Massenspektrometrie
Mit Hilfe der Massenspektrometrie kann die Teilchendichte einer Spezies im Plasma bestimmt werden.
Inhaltsverzeichnis
Messprinzip
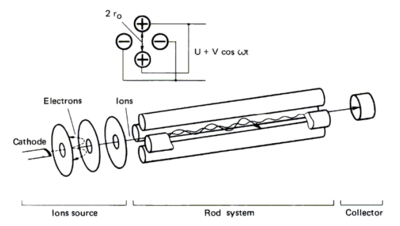
Durch Massenspektrometrie kann das Masse/Ladungs-Verhältnis (m/q) eines Teilchens bestimmt werden. Das Messprinzip beruht auf Ionisation von Neutralteilchen, wodurch Ionen entstehen, die durch ein elektrisches Feld nach dem Masse/Ladungs-Verhältnis gefiltert werden. Da die Teilchen im Spektrometer nicht mit Hintergrundmolekülen zusammenstoßen dürfen, benötigt man einen geringen Druck innerhalb des Spektrometers, um eine große freie Weglänge der Teilchen zu gewährleisten. Eine Vakuumtrennung zwischen Plasma und Massenspektrometer ist nötig, da das Plasma in der Regel bei vergleichsweise hohen Drücken betrieben wird. Hinter zwei Pumpstufen zur Vakuumtrennung befindet sich der Ionisator. In diesem Versuch wird ein Crossbeam-Ionizer verwendet, der die Neutralteilchen senkrecht zur ihrer Flugrichtung mit Elektronen beschießt und dadurch ionisiert. Der Ionisationswirkungsquerschnitt ist von der verwendeten Elektronenenergie und den zu ionisierenden Teilchen abhängig. Ein Maximum für die meisten Teilchen befindet sich bei 70eV. Mit Hilfe eines Quadrupolfeldes werden die Ionen nach ihrem Masse/Ladungs-Verhältnis sortiert und auf einen Detektor gelenkt. Aus den Signalstärken der einzelnen Masse/Ladungs- Verhältnisse, kann die Teilchendichte der jeweiligen Spezies bestimmt werden. Vor dem Massenspektrometer befindet sich ein Chopper, mit dem es möglich ist Beiträge des Hintergrundgases zu messen. Die unterschiedlichen Möglichkeiten Spezien in Spektren zu identifizieren werden im Folgenden erläutert.
Fragmentierungsmuster
Werden Messungen mit einer Elektronenenergie von 70 eV im Ionisator durchgeführt, können Neutralteilchen mehrfach ionisiert werden, sowie Bruchstück-Ionen mit unterschiedlicher Häufigkeit erzeugt werden. Daraus ergibt sich ein, für die jeweilige Spezies charakteristisches Fragmentierungsmuster.
Um zum Beispiel ein 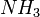 -Molekül zu ionisieren ist eine Elektronenenergie von 10,05 eV nötig. Das ionisierte Teilchen wird bei 17 amu detektiert. Bei hohen Elektronenenergien kann das Bruchstück-Ion NH
-Molekül zu ionisieren ist eine Elektronenenergie von 10,05 eV nötig. Das ionisierte Teilchen wird bei 17 amu detektiert. Bei hohen Elektronenenergien kann das Bruchstück-Ion NH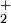 erzeugt werden, welches bei 16 amu nachgewiesen wird. Ebenso kann eine Dissoziation in die Ionen
erzeugt werden, welches bei 16 amu nachgewiesen wird. Ebenso kann eine Dissoziation in die Ionen 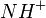 und
und 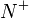 mit 15 amu bzw. 14 amu erfolgen.
Die Signalstärke sinkt, je größer die Ionisationsenergie ist. Das Verhältnis der Peaks zueinander ist für eine Spezies konstant.
mit 15 amu bzw. 14 amu erfolgen.
Die Signalstärke sinkt, je größer die Ionisationsenergie ist. Das Verhältnis der Peaks zueinander ist für eine Spezies konstant.
Schwellenspektroskopie
Bei einer Gasmischungen können mehrere Teilchen Signale bei gleichem Masse/Ladungs-Verhältnis erzeugen. Um den Signalanteil eines einzelnen Radikals nachzuweisen, wird die Schwellenspektroskopie durchgeführt. Es wird ausgenutzt, dass die Moleküle unterschiedliche Ionisationsenergien besitzen.\\ Wiederum wird anhand des Beispiels Ammoniak das Prinzip der Schwellenspektroskopie erklärt. Es treten folgende Reaktionen auf:
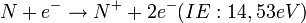
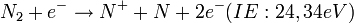
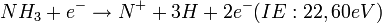
Alle Reaktionen haben die Bildung von 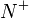 (14 amu) zur Folge. Wird die Energie der Elektronen im Ionisator knapp unter 22,60 eV reduziert, kann ausschließlich die erste der dargestellten Reaktionen stattfinden, da die Energie zur Bildung von
(14 amu) zur Folge. Wird die Energie der Elektronen im Ionisator knapp unter 22,60 eV reduziert, kann ausschließlich die erste der dargestellten Reaktionen stattfinden, da die Energie zur Bildung von 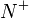 aus
aus 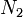 bzw.
bzw. 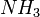 nicht ausreicht. Das gemessene Signal stammt dann aus der Ionisation von molekularem Stickstoff.
nicht ausreicht. Das gemessene Signal stammt dann aus der Ionisation von molekularem Stickstoff.
Bestimmung der Teilchendichte aus einem gemessenen Spektrum
Die Bestimmung der Teilchendichte im Plasmareaktor kann über das gemessene Signal erfolgen:
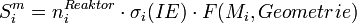
Das Signal S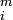 setzt sich aus der Teilchendichte des Moleküls im Reaktor, sowie dessen Wirkungsquerschnitt
setzt sich aus der Teilchendichte des Moleküls im Reaktor, sowie dessen Wirkungsquerschnitt 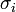 bei der entsprechenden Ionisationsenergie im Ionisator zusammen. Der Faktor F ist von der jeweiligen Reaktorgeometrie und der detektierten Masse abhängig.
Die Betrachtung zweier Signale unterschiedlicher Moleküle liefert:
bei der entsprechenden Ionisationsenergie im Ionisator zusammen. Der Faktor F ist von der jeweiligen Reaktorgeometrie und der detektierten Masse abhängig.
Die Betrachtung zweier Signale unterschiedlicher Moleküle liefert:
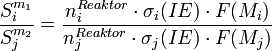
Liegen die Massen der untersuchten Moleküle nahe beieinander, kürzt sich der Faktor 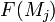 mit
mit 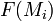 zu eins.
zu eins.
--Gina Oberbossel+Marina Prenzel 17:56, 27. Mär. 2010 (UTC)