Grundlagen
\chapter{Grundlagen}
\textbf{Anmerkung:} Die Grundlagen der Plasmaphysik in diesem Kapitel können ausführlicher in \cite{plasma} (Kapitel 7+8) nachgelesen werden.\\ Die Grundlagen der Massenspektrometrie in diesem Kapitel können ausführlicher in \cite{pww} (Kapitel 3.2) nachgelesen werden.
\section{Niedertemperatur-Niederdruck-Plasmen}
Plasmen der Plasmatechnik können auf unterschiedliche Art und Weise erzeugt werden. Allen Methoden ist gemein, daß Elektronen in statischen oder oszillierenden elektrischen Feldern beschleunigt werden. Ist die Beschleunigung so stark, dass Elektronen-Stoß-induzierte Reaktionen in ausreichender Rate zur Ionisation des Neutralgases führen, kann ein Plasma zünden. Im Plasmazustand entsteht ein Gleichgewicht aus Ionisation und den Verlusten der Ladungsträger durch Diffusion und Rekombination.
Ein Plasma zeichnet sich dadurch aus, daß die Zahl der positiven und negativen Ladungsträger nahezu gleich ist. Es herrscht Quasineutralität. Nachdem Elektronen wegen ihrer höheren Beweglichkeit ($m_{el}=\frac{1}{1836}m_{ion}$) ein Plasma leichter verlassen können, baut sich am Rand des Plasmas eine Potentialdifferenz auf, um dem Verlust der Elektronen entgegen zu wirken. Dies bezeichnet man als Randschicht. Die elektrischen Felder sind in dieser Randschicht in der Regel groß, während sie im Plasmavolumen wegen der Quasineutralität klein sind. Damit ist ein Plasma immer elektrisch positiv im Vergleich zu den umgebenden Wänden.
In den Plasmen der Plasmatechnik, die bei niedrigem Druck erzeugt werden, werden oftmals nur die Elektronen durch die oszillierenden elektrischen Felder geheizt. Diese erreichen Temperaturen bis mehrere 10000 K. Die Ionen und die Neutralteilchen bleiben in der Regel kalt. Diese Plasmen werden als Niedertemperatur- und Niederdruck-Plasmen bezeichnet.
Ein besonders wichtiger Entladungstyp sind Plasmen, die mit oszillierenden elektrischen Feldern erzeugt werden. Sogenannte {\bf rf}-Entladungen ({\bf r}adio {\bf f}requency) oder Hochfrequenz-Entladungen. In der Plasmatechnik werden Frequenzen von typischerweise 13.56 MHz gewählt. Dieser Entladungstyp wird auch in diesem Versuch betrachtet. Ein Vorteil der Verwendung von Hochfrequenz ist die Möglichkeit Dielektrika als Elektroden benutzen zu können. Im Fall von Gleichstromentladung führt die Aufladung der Oberflächen dazu, dass innerhalb der Dielektrika große Feldstärken erreicht werden. Diese hohen Feldstärken führen zu Überschlägen innerhalb der Dielektrika und damit zu deren Zerstörung.
Man kann rf-Entladungen in zwei Kategorien einteilen: Kapazitive und induktive Entladungen. Der Typ wird durch die Art der Leistungseinkopplung in das Plasma bestimmt.
\subsection{Die kapazitive rf-Entladung}
Der einfachste Aufbau einer rf-Entladung ist ein
Plattenkondensator in einem Vakuumgefäß an den ein rf-Generator
angeschlossen ist. Diese Art der Plasmaerzeugung wird auch {\bf
C}apacitively {\bf C}oupled {\bf P}lasma genannt. Zwischen den
Kondensatorplatten wird ein sich zeitlich veränderndes
hochfrequentes elektrisches Feld erzeugt. Elektronen, leichter und
beweglicher als Ionen, sind in der Lage dem Feld zu folgen und
oszillieren. Schnelle Elektronen erzeugen durch Stoßionisation
weitere Ionen und Elektronen und zünden somit das Plasma. In
dieser Art von Entladung entsteht in der Randschicht des Plasmas
eine große Potentialdifferenz in der die Ionen stark beschleunigt
werden und mit hoher Energie auf das Substrat aufschlagen und es
sogar zerstören können. Dieses Phänomen wird Ion Bombardment
genannt. In diesen Plasmen hängt sowohl die Elektronendichte als
auch die Randschichtspannung von der angelegten HF-Leistung ab.
Man kann deshalb die Elektronendichte nicht beliebig erhöhen, da
gleichzeitig auch das Ion Bombardement steigt.
\begin{figure}[h] \begin{center} \includegraphics*[width = 8 cm]{bilder/kap8_9.eps} \caption{Kapazitive rf Entladung} \label{fig:kap8_9} \end{center} \end{figure}
\subsection{Die induktive rf-Entladung} Bei induktiven Entladungen ({\bf I}nductively {\bf C}oupled {\bf P}lasma) wird ohne Elektrode über eine Spule und einem Dielektrikum (Quartz-Fenster) ein elektrisches Feld im Plasma induziert. Das Plasma stellt dabei eine einzelne Sekundärwicklung eines Transformators dar. Für diese induktive Einkopplung gibt es zylindrische oder planare Konfigurationen. Die äußere Primärspule erzeugt ein veränderliches Magnetfeld, das in der \glqq Sekundärspule\grqq~ Plasma ein elektrisches Feld induziert. Dies treibt den Strom im Plasma. Der Verschiebungsstrom fließt im induktiven Fall im wesentlichen parallel zu dem Dielektrikum, während er im kapazitiven Fall normal zum Dielektrikum verläuft (siehe Abb. \ref{fig:kap8_13}).
\begin{figure}[h] \begin{center} \includegraphics*[width = 10 cm]{bilder/kap8_13.eps} \caption{Unterschied zwischen einer induktiven und einer kapazitiven Kopplung} \label{fig:kap8_13} \end{center} \end{figure}
Die absorbierte Leistung im Plasma hängt von der Effizienz des Transformators ab und dem Volumen in dem der Plasmastrom fließt. ICPs koppeln die Energie effizienter als CCPs in das Plasma ein. Dadurch lassen sich auch dichtere Plasmen mit ICPs erzeugen. Hinzu kommt noch, dass die Randschichtspannung in diesen Plasmen geringer ist. Deshalb ist es möglich die Elektronen- und Ionenenergie seperat durch HF-Leistung und zusätzlich angelegter Vorspannung am Substrat (Biasspannung) einzustellen.
\subsubsection{E-Mode, H-Mode, E-H-Hysterese}
Neben dem induziertem E-Feld der \glqq Sekundärwicklung\grqq~ Plasma, sehen die Ladungsträger auch das elektrische Feld der leitfähigen Spule direkt. In diesem Feld werden sie ähnlich geheizt wie in einem CCP. Dies wird sichtbar bei geringen HF-Leistungen, bei denen die Effizienz des Transformators noch gering ist. Ein im Vergleich zur induktiven Entladung schwach leuchtendes Plasma entsteht. Die elektrischen Felder die durch den Spannungsabfall in der Spule hervorgerufen werden, sind hierfür verantwortlich. Es liegt also eine kapazitive Entladung vor und man spricht vom E-Mode. Erhöht man die HF-Leistung auf einen bestimmten Wert, wird das Plasma sprungartig heller und dichter. Die Entladung ist jetzt größtenteils induktiv und man nennt dies H-Mode. Eine weitere Erhöhung der Leistung, erhöht zwar die Plasmadichte und damit auch die Helligkeit, aber es gibt keinen abrupten Sprung mehr. Verringert man die HF-Leistung wieder, erwartet man einen Übergang vom H-Mode in den E-Mode bei der selben Leistung wie beim E-H-Übergang. Jedoch wechselt die Entladung bei einer kleineren HF-Leistung in den E-Mode zurück (abrupte Abnahme der sichtbaren Emission). Dieser Vorgang wird als E-H-Hysterese bezeichnet und ist Gegenstand aktueller Forschungen. Anzumerken ist noch, dass bei einer induktiven Entladung E- und H-Mode gleichzeitig existieren.
\section{Massenspektrometrie}
Der Nachweis von Teilchen mit einem Massenspektrometer basiert auf der Kontrolle einer Teilchentrajektorie eines Ions in einem bekannten System aus elektrischen und magnetischen Feldern. Für den Nachweis von Neutralteilchen müssen diese zunächst ionisiert werden. Weiterhin darf es in einem Massenspektrometer nicht zu Stößen mit dem Neutralgas kommen. Letzteres erfordert in der Regel einen Druck besser als 10$^{-5}$ mbar. Nachdem Plasmen in der Regel bei höheren Drücken betrieben werden, benötigt man ein getrenntes Vakuumsystem für das Plasma und das Massenspektrometer.
Nach der Ionisation eines Neutralteilchens muß das entstehende Ion nach seiner Masse gefiltert werden. Ein kompaktes Massenfilter ist ein Quadrupol, der auf oszillierenden elektrischen Feldern basiert.
\begin{figure}[h]
\begin{center}
\includegraphics*[width = 9 cm]{bilder/Aufbau.eps}
\caption{Typischer Aufbau eines Quadrupols in einer differentiellen
Pumpstufe in einem ICP (Versuchsaufbau)} \label{fig:icpms1}
\end{center}
\end{figure}
Die wesentlichen Komponenten eines typischen Massenspektrometers, wie es in der Plasmatechnik zum Einsatz kommt sind: eine differentielle Druckstufe, ein Ionisator, ein Quadrupol und ein Detektor, wie in Abb. \ref{fig:icpms1} und \ref{fig:msschema} illustriert. Die Funktionsweise der einzelnen Komponenten werden im folgenden beschrieben.
\begin{figure}[h]
\begin{center}
\includegraphics*[width = 8 cm]{bilder/msschema.eps}
\caption{Schema der einzelnen Komponenten eines MS}
\label{fig:msschema}
\end{center}
\end{figure}
\subsection{Die differentielle Pumpstufe}
Der Druck in einem Massenspektrometer sollte so klein wie möglich sein um Beiträge zum Hintergrund durch Dissoziation an den heissen Filamenten im Ionisator zu reduzieren. Weiterhin muß die freie Weglänge der Teilchen größer als die Dimension des Spektrometers sein. Schließlich arbeitet der Detektor, ein Secondary Electron Multiplier (s. Kap. \ref{sec:SEM}), nur bei Drücken unterhalb 10$^{-6}$ mbar. Dies macht eine Vakuum-Trennung zwischen Plasma und Massenspektrometer notwendig. Durch die Extraktionsöffnung werden die Teilchen aus dem Plasma in das Massenspektrometer geführt. Mann möchte eigentlich eine große Öffnung verwenden, damit eine hohe Intensität erreicht wird. Dies würde aber das Vakuum deutlich verschlechtern. Um trotzdem eine größere Extraktionsöffnung verwenden zu können, installiert man weitere (differentielle) Pumpstufen\footnote{Auch diese Pumpstufen haben Extraktionsöffnungen. Alle Öffnungen müssen so angeordnet sein, dass sie auf einer Geraden liegen, die in Richtung Ionisator zeigt Dies ermöglicht es dem Teilchenstrahl ungehindert ins MS zu gelangen.} zwischen Massenspektrometer und Plasma und setzt das Massenspektrometer in die zweite oder dritte Stufe. Mehr Stufen aber reduzieren das Signal wieder, da der Abstand zwischen Plasma und Ionisator groß wird. Es gilt also ein Optimum aus Öffnungsradien und Anzahl der Pumpstufen und Abstand des Massenspektrometers zum Plasma zu finden, um das MS-Signal möglichst groß zu machen.
\subsection{Der Ionisator}
Für den Nachweis werden gesammelte Neutralteilchen zunächst in einem Ionisator ionisiert. Hierbei gibt es mehrere Bauformen. Ein idealer Ionisator führt zu einer Elektronenstoß-Ionisation der einfallenden Neutralen bei einer festgelegten Energie. Als Elektronen-Emitter kommt ein heisses Filament zum Einsatz, das gegenüber einem Ionisationsvolumen auf negatives Potential gelegt wird, um die Elektronen zu beschleunigen (siehe Abb. \ref{fig:kap3_4m}). In diesem Versuch wird ein sogenannter Crossbeam-Ionizer verwendet, bei dem die Elektronen senkrecht zum Neutralteilchenstrahl emittiert werden. Die Anzahl erzeugter Ionen $n_{ions}$ pro Sekunge hängt von der Neutralteilchendichte $n_{neut}$, dem Emissionsstrom $I_{e}$ (aus dem Filament emittierter Elektronenstrom) und dem Elektronen-abhängigen Ionisationswirkungsquerschnitt ${\sigma}_{ion}(E_{el})$ ab.
\begin{equation}
\mathrm{MS\texttt{-}Signal} \sim \frac{dn_{ions}}{dt} \sim n_{neut}{\cdot}I_{e}{\cdot}{\sigma}_{ion}(E_{el})
\end{equation}
\begin{figure}[h] \begin{center} \includegraphics*[width = 7 cm]{bilder/kap3_6.eps} \caption{Schema einer Crossbeam-Quelle} \label{fig:kap3_4m} \end{center} \end{figure}
Der Ionisations-Wirkungsquerschnitt ${\sigma}(E_{el})$ ist für einige Gase in Abb. \ref{fig:sigma} dargestellt. Er ist Null für Energien unterhalb einer gewissen Schwelle (Ionisationspotential), die, abhängig von der Spezies, bei etwa $8 \eV$ bis $25 \eV$ liegt. Der Querschnitt steigt dann bis auf ein Maximum, dass etwa bei $70 \eV$ (Standardwert) liegt und fällt für hohe Energien wieder ab. Arbeitet man mit Elektronenenergien nahe am Ionisationspotential, kann man reaktive Radikalteilchen detektieren (siehe Schwellwert-Spektroskopie).
\begin{figure}[h] \begin{center} \includegraphics*[width = 10 cm]{bilder/sigma.eps} \caption{Ionisations-Wirkungsquerschnitt verschiedener Spezies} \label{fig:sigma} \end{center} \end{figure}
Durch Verwendung von Elektronenenergien größer als $20 \eV$ kommt es aber zur Fragmentierung der Moleküle. Dadurch bekommt man im Massenspektrum auch Peaks bei den Massen der Bruchstück-Ionen.
\subsubsection{Fragmentierung, Mehrfachionisierung, Isotope}
Die Elektronen-Energie in einem Ionisator ist in der Regel $70 \eV$. Bei dieser Energie durchlaufen die Ionisations-Wirkungsquerschnitte für die meisten Verbindungen ihr Maximum (s.o.). Sie ist aber größer als die Bindungsenergie der Moleküle. D.h. es wird im Ionisator nicht nur das primäre Mutter-Ion durch Stoßionisation gebildet, sondern abhängig von der Elektronenenergie, eine ganze Reihe von Bruchstück-Ionen (Dissoziation) mit unterschiedlicher Häufigkeit ein sog. Fragmentierungsmuster (Cracking Pattern) entsteht.
Diese Fragmentierungsmuster überlappen sich im Massenspektrum. Um aus diesen Daten wieder die Dichten der ursprünglichen Neutralteilchen zu extrahieren, müssen die Spektren wieder in die Einzelbeiträge zerlegt werden.
Dies sei am Beispiel eines Methanmoleküls illustriert. Durch Ionisation und Dissoziation im Ionisator enstehen folgende Ionen:
\begin{eqnarray} \nonumber {\rm CH_4 + e^-} &\rightarrow& {\rm CH_4^+ + 2 e^-}\\ \nonumber {\rm CH_4 + e^-} &\rightarrow& {\rm CH_3^+ + H + 2 e^-}\\ \nonumber {\rm CH_4 + e^-} &\rightarrow& {\rm CH_2^+ + H_2 + 2 e^-}\\ \nonumber {\rm CH_4 + e^-} &\rightarrow& {\rm CH^+ + H_2 + H + 2 e^-} \end{eqnarray}
\begin{figure}[h] \begin{center} \includegraphics*[width = 8 cm]{bilder/ch4cracking.eps} \caption{Fragmentierung eines Methanmoleküls im Ionisator des Massenspektrometers.} \label{fig:ch4cracking} \end{center} \end{figure}
Dazu kommen noch andere Effekte, die im Massenspektrum weitere
Peaks erzeugen. Jedes Atom hat Isotope. Da sie sich in ihrer
Atommasse unterscheiden werden sie auch bei unterschiedlichen
Masse/Ladungs-Verhältnissen regristriert. So erzeugt z.B ein
Ar-Atom bei einer Elektronenenergie von $70 \eV$ ein Signal bei
M/Z=20,36,38 und 40. Die Peaks bei 36, 38 und 40 repräsentieren
die unterschiedlichen Argon-Iosotope Ar$^{36+}$, Ar$^{38+}$ und
Ar$^{40+}$. Der Peak an der Stelle 20 wird durch
Mehrfachionisation des Ar-Atoms hervorgerufen (Ar$^{40++}$). Hier
ergibt sich gerade ein Masse/Ladungsverhältnis von 40/2=20.
Mehrfach ionisiertes Ar$^{36}$ und Ar$^{38}$ wird in der Regel
wegen zu kleiner Intensitäten nicht registriert.
Jede Spezies hat ein charakteristisches Fragmentierungsmuster, das mit einem gegebenen Aufbau gemessen werden kann. Es ist aber nötig, das MS mit einem Satz bekannter Spezies mit bekannter Dichte zu kalibrieren. Dadurch kann man erst akurate Daten einer unbekannten Gasmischung erhalten.
\subsection{Massenfilter}
Der Massenfilter eines Quadrupol-Massenspektrometers besteht aus einem Stabsystem aus 4 zylindrischen, parallelen Stäben\footnote{Die absolute Oberflächengenauigkeit der Stäbe ist fertigungs-technisch festgelegt (typisch $\mu$m). Der absolute Durchmesser der Stäbe (mehrere mm) bestimmt damit, bis zu welcher Genauigkeit das elektrischen Feld auf der Achse realisiert werden kann.}, wobei die gegenüberliegenden Stäbe gleich beschaltet sind, wie in Abb. \ref{fig:kap2_23} gezeigt ist. Das axiale Quadrupolfeld hat die Form:
\begin{equation} \Phi(x,z) = \frac{\Phi_0}{2r_0^2}\left(x^2-z^2\right) \end{equation}
\begin{figure}[h] \begin{center} \includegraphics*[width = 7 cm]{bilder/kap2_23.eps} \caption{Quadrupol-Massenspektrometer} \label{fig:kap2_23} \end{center} \end{figure}
An dieses Stabsystem wird ein elektrisches Wechselfeld $\Phi_0$ angelegt, das durch einen Gleichspannungsanteil $U$ und einen Wechselspannungsanteil $V$ charakterisiert ist.
\begin{equation} \Phi_0 = U + V \cos \omega t \end{equation}
Die Bewegungsgleichungen eines geladenen Teilchens der Ladung $q$ und Masse $m$, das sich durch diesen Filter in axialer Richtung bewegt, ist gegeben als:
\begin{equation} \frac{d^2x}{dt^2}+\frac{q}{mr_0^2}(U + V\cos\omega t)x = 0 \end{equation}
\begin{equation} \frac{d^2z}{dt^2}-\frac{q}{mr_0^2}(U + V\cos\omega t)x = 0 \end{equation}
Diese Bewegungsgleichung läßt sich kompakter formulieren, nachdem man folgende neue Größen eingeführt hat:
\begin{equation} a = \frac{4 q U}{m r_0^2 \omega^2} \end{equation}
\begin{equation} b = \frac{2 q V}{m r_0^2 \omega^2} \end{equation}
\begin{equation} \tau = \frac{1}{2} \omega t \end{equation}
Damit erhält man die sog. {\bf Mathieu'sche Differentialgleichungen}:
\begin{eqnarray} \frac{d^2x}{d\tau^2}+(a+2b \cos 2 \tau) x &=& 0 \\ \frac{d^2z}{d\tau^2}-(a+2b \cos 2 \tau) z &=& 0 \end{eqnarray}
Diese Gleichungen haben stabile Lösungen für die Trajektorie eines Teilchens im Stabsystem in Abhängigkeit von der Wahl der Parameter $a$ und $b$. Dies ist in Abb. \ref{fig:kap3_2m} verdeutlicht.
\begin{figure}[h] \begin{center} \includegraphics*[width = 6 cm]{bilder/kap2_24.eps} \caption{Stabilitätsdiagramm für die Trajektorie in einem Quadrupol-Massenspektrometer.} \label{fig:kap3_2m} \end{center} \end{figure}
Wird das Verhältnis aus Gleich- und Wechselspannungsanteil
konstant gehalten, bekommt man eine Gerade in dem
Stabilitätsdiagramm. Die absolute Wahl, z. B. der Gleichspannung
bei konstantem Verhältnis $\frac{a}{b}$ bestimmt die Masse des
Ions, das den Filter passieren kann:
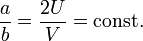
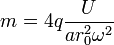
D. h. auf dieser Geraden liegen die Arbeitspunkte für bestimmte Massen. Liegt einer dieser Punkte in dem Stabilitätsbeich (Abb. \ref{fig:kap3_3m}) kann die dazu gehörende Masse den Filter passieren, alle anderen Massen haben instabile Bahnen und werden separiert.
Will man die Massenauflösung erhöhen, kann man das Verhältnis aus Gleich- und Wechselspannungsanteil verändern und schränkt somit die Zahl der zulässigen Trajektorien ein, wie es in Abb. \ref{fig:kap3_3m} gezeigt ist.
\begin{figure}[h] \begin{center} \includegraphics*[width = 7 cm]{bilder/kap2_25.eps} \caption{Gebiet der zulässigen Trajektorien bei gegebenem Verhältnis zwischen Gleich- und Wechselspannungsamplitude, $m_3>m_2>m_1$.} \label{fig:kap3_3m} \end{center} \end{figure}
Ein Massenscan wird realisiert, in dem man bei konstantem Verhältnis von $U$ und $V$ die Amplituden beginnend von kleinen Werten von $U$ und $V$ erhöht. Damit wandern die Arbeitspunkte (entspricht den Massen) sukzessiv durch den Stabilitätsbereich.
Die Geschwindigkeit mit der Ionen durch diesen Quadrupolfilter einer Länge $L$ laufen, bestimmt die Massentrennung, die man erreichen kann. Die instabilen Bahnen zeichnen sich dadurch aus, das die Amplituden der Oszillationsbewegung in dem Quadrupolfeld exponentiell ansteigen. Bei kleiner Abweichung der Masse von der Sollmasse für die die Transmissisonsbedingung erfüllt ist, erfolgt der exponentielle Anstieg der Amplitude nur langsam. D.h. die Massenauflösung wird besser wenn das Stabsystem länger gemacht wird. Falls die Geschwindigkeit der Ionen groß ist, hat die Trajektorie bei gegebener Länge nicht die Möglichkeit viele rf-Zyklen des Quadrupolfeldes zu durchlaufen und der exponentielle Anstieg der Amplitude kann nicht ausreichen, um das Ion dauerhaft abzulenken. Demnach ist für die Massenauflösung, die {\it Verweilzeit} des Ions im Quadrupolfilter ausschlaggebend. Wird demnach die Geschwindigkeit der Ionen zu klein, werden sie anfällig für Abweichungen von dem idealen Quadrupolfeld und verlieren den Einschluss, bzw. lassen sich durch die Optiken nicht mehr gut kontrollieren. Es muß deshalb ein Kompromiss gefunden werden zwischen stabilen Trajektorien und erreichbarer Massenauflösung. Die Größe des Stabsystems, bestimmt im wesentlichen die erreichbare Auflösung, da es bei größeren Stäben einfacher ist die erforderliche Oberflächenrauhigkeit im Bereich $\mu m$ zu realisieren, die notwendig ist um ein auf der Achse ideales Quadrupolfeld zu erzeugen.
\subsection{Ionen-Nachweis}\label{sec:SEM}
Der Nachweis der Ionen erfolgt über Sekundärelektronen-Erzeugung in einem Channeltron oder in einem Secondary Electron Multiplier (Abb. \ref{fig:sem}). Ihre Effizienz hängt von der Geschwindigkeit der Ionen ab, und demnach wird bei höheren Massen bei gleicher Energie, der Nachweis immer unempfindlicher. Dies muß erst durch Kalibrierung bestimmt werden. Verwendet man einen Faraday-Detektor (Abb. \ref{fig:faraday}), so ist dieser gegenüber der Geschwindigkeit der Ionen unempfindlich. Allerdings ist die Sensitivität des Faraday-Detektors sehr viel geringer als die eines SEM. Zudem ist der Faraday-Detektor langsamer als ein SEM. Schließlich hängt es von der Bauform dieses Faraday-Cups ab, ob die ioneninduzierten Sekundärelektronen innerhalb dieses Faradaydetektors gefangen bleiben. Manchmal wird vom jeweiligen Hersteller nur ein einfaches Blech im Strahlengang als Faraday-Detektor bezeichnet, obwohl dort der Einfang der Sekundärelektronen {\it nicht} gewährleistet ist.
Die Performance eines SEM kann stark variieren mit der Belegung der jeweiligen Oberflächen, dass diese Belegung die Austrittsarbeit ändert und damit die Effizienz für die Produktion von Sekundärelektronen. Deshalb ist es notwendig das SEM Signal {\it täglich} mit dem Signal des Faraday-Detektors oder eines anderen Standards sehr häufig zu kalibrieren.
\begin{figure}[h] \begin{center} \includegraphics*[width = 8 cm]{bilder/sem.eps} \includegraphics*[width = 6 cm]{bilder/channeltron.eps} \caption{Schema eines SEM (oben) und Channeltron (unten)} \label{fig:sem} \end{center} \end{figure}
\begin{figure}[h] \begin{center} \includegraphics*[width = 8 cm]{bilder/faraday.eps} \caption{Schema eines Faradaydetektors.} \label{fig:faraday} \end{center} \end{figure}
\subsection{Ionisations-Schwellen-Massenspektrometrie}
Die Energie im Ionisator ist zumeist $70\, \mathrm{eV}$. Um die Fragmentierung zu reduzieren wird bei der Ionisations-Schwellen-Massenspektrometrie (auch {\bf T}reshold {\bf I}onisation {\bf M}ass {\bf S}pectrometry genannt) die Energie der Elektronen im Ionisator reduziert. Der Nachteil ist allerdings, daß das Signal um Größenordnungen kleiner ist. Mit dieser Methode ist es möglich, den Beitrag von Radikalen in einem Teilchenstrom von dem der neutralen Muttermoleküle zu unterscheiden. Man nutzt den Umstand aus, daß z. B. folgende Reaktionen eine unterschiedliche Schwellenenergie haben:
\vspace{0.5cm} \begin{tabular}{rll}
CF$_3+e^-$ (E$_{el}$ $>$ $ 8.9 \eV$)& $\rightarrow$ CF$_3^+ + 2e^-$ & direkte Ionisation \\
CF$_4+e^-$ (E$_{el}$ $>$ $15.9 \eV$)& $\rightarrow$ CF$_3^+ + {\rm F} + 2e^-$ & dissoziative Ionisation \\
\end{tabular} \vspace{0.5cm}
Die Schwellenenergie der ersten Reaktion liegt bei $8.9 \eV$ (reine Ionisation) während die der zweiten Reaktion bei $15.9 \eV$ liegt, da zusätzlich zur Ionisation noch ein C-F Bindungsbruch stattfindet. D.h. stellt man die Elektronen-Energie auf einen Wert zwischen 9 und $15 \eV$ so erhält man auf dem Massenkanal 15 amu nur Beiträge von CF$_3$ Radikalen. In Abb. \ref{fig:tims} ist ein TIMS-Messung von CF$_4$ mit und ohne Plasma abbgebildet. Das TIMS-Verfahren kann auch verwendet werden um Ionisations- und Dissoziationsenergien von verschiedenen Stoffen zu finden.
\begin{figure}[h] \begin{center} \includegraphics*[width = 14 cm]{bilder/tims.eps} \caption{Beispiel einer CF$_3$-Radikalenmessung in einem CF$_4$-Plasma (aus \cite{coburn} entnommen). Der Ausschlag bei Elektronenenergien unterhalb von $15.9 eV$ entsteht durch direkte Ionisation von CF$_3$-Radikalen. Ausschläge bei Energien größer $15.9 eV$ kommen durch direkte Ionisation von CF$_3$ sowie durch Dissoziation von CF$_4$ -Molekülen zustande. Die Abnahme des Signals bei eingeschaltetem Plasma läßt sich durch die Umwandlung von CF$_4$ in andere Moleküle erklären (Verbrauch). Der Chopper ermöglicht es Beiträge des Hintergrundgases zu messen.} \label{fig:tims} \end{center} \end{figure}