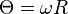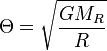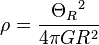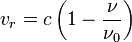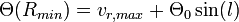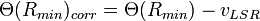Dunkle Materie in der Milchstraße?
Versuchsnummer: 601
Kontakt: Priv.-Doz. Dr. Dominik Bomans --- e-Mail: bomans@astro.rub.de --- Raum GAFO 03/973 --- Telefon: 0234 32 22335
Betreuer: Dr. Peter Kamphuis --- Raum GAFO 03/954
WICHTIG: Der Versuch steht ab Dezember 2019 wieder zur Verfügung. Beobachtungen werden vorerst Remote mit Radioteleskopen in den Niederlanden oder Polen durchgeführt, bis eine lokales Radioteleskop am neuen Campus Observatorium in Betrieb geht. Wegen des signifikanten Zeitaufwandes für die Datenreduktion ist dieser Versuch ür 2 CP im FP anrechenbar. Vor der Buchung dieses Versuchs sollte unbedingt eine Terminabsprache per Mail erfolgen, da die Milchstraße zum gewünschten Termin schließlich auch hoch am Himmel stehen muss.
Die Existenz Dunkler Materie gilt als eines der großen Rätsel moderner Astronomie und Physik. Diese seltsame Form von Materie macht sich ausschließlich durch ihre gravitative Wechselwirkung bemerkbar und entzieht sich bislang der direkten Beobachtung mit konventionellen Teleskopen oder in Beschleuniger-Experimenten. Ihre gravitative Wechselwirkung ist jedoch erstaunlich einfach zu beobachten, was in diesem Versuch, der im Übrigen genau so vor ca. 40 Jahren zum Postulat Dunkler Materie geführt hat, geschehen soll. Mit dem 3m-Radioteleskop des Astronomischen Instituts auf dem Dach des NA-Gebäudes kann der Hyperfeinstruktur-Übergang des neutralen Wasserstoffs in der Milchstraße gemessen und aus dessen Verteilung auf fehlende - daher "dunkle" - Materie geschlossen werden, die nötig ist, um die Beobachtungen zu erklären. Im Versuch werden die folgenden Aspekte angegangen:
- Umgang mit einem motorisierten und computergesteuerten Teleskop
- charakteristische Größen eines Teleskops (Empfindlichkeit, Auflösungsvermögen)
- Planung und Durchführung eines geeigneten Messprogramms
- stat. Datenauswertung
Inhaltsverzeichnis
Einleitung
Von Dunkler Materie hat wohl Jeder schon einmal etwas gehört. Versteckt, geheimnisvoll, eben völlig dunkel soll sie unser Universum erfüllen und dort für einen großen Teil der Gravitation sorgen. Ohne sie wäre es überhaupt nicht so schnell zur Bildung von Sternen, Galaxien und Haufen gekommen, sodass wir alle heute nicht existieren würden, sagen uns die Kosmologen. Nicht so glücklich mit ihr sind hingegen die Teilchenphysiker, deren größte Aufgabe es zur Zeit ist, ihr endlich das dunkle zu nehmen und ein Elementarteilchen zu präsentieren, aus dem sie besteht.
Fest steht nur (mit nahezu absoluter Sicherheit), dass es Dunkle Materie wirklich gibt. Dafür sprechen zahlreiche Messungen und auch theoretische Überlegungen zur Dunklen Materie vor allem im frühen Universum. Doch was sind das für Messungen? Kann man sie überhaupt nachvollziehen, sodass sich jeder (mit relativ geringem Aufwand) von den Ergebnissen überzeugen kann? Diese Fragen sollen mit diesem Versuch zumindest teilweise geklärt werden, indem genau die Messung nachempfunden wird, die zum Postulieren von Dunkler Materie geführt hat: Die Vermessung der Rotationsgeschwindigkeit(en) von Galaxien.
Die erste Galaxie, die es sich lohnt, zu untersuchen, ist natürlich unsere eigene, die Milchstraße. Darüber hinaus bietet sie sich auch an, weil wir uns direkt in ihr befinden, ihre Strahlung sollte also die stärkste und damit leicht zu beobachten sein. Die grundsätzliche Vorgehensweise ist jedoch auch bei externen Galaxien nicht anders, jedoch muss hier erheblich mehr Aufwand getrieben werden.
Bleibt nur noch die Frage, welche Art von Strahlung sich am besten zur Ableitung einer Rotationskurve (Rotationsgeschwindigkeit aufgetragen gegen die Entfernung vom galaktischen Zentrum) eignet. Sie müsste idealer Weise über die gesamte Ausdehnung der Milchstraße sichtbar sein, sodass von jedem Ort Daten erhoben werden können. Messungen im optischen Wellenlängenbereich scheiden also schon einmal aus, genau so wie noch kurzwelligere Strahlung. Doch die Natur meint es gut mit den Astronomen, denn sie hat das ideale Werkzeug für unsere Anforderungen bereit gestellt: die 21 cm Strahlung von neutralem Wasserstoff, auch H I genannt.
Warum ist gerade diese 21 cm Strahlung für unsere Beobachtung so geeignet im Vergleich zu anderen Wellenlängen und wodurch erkaufen wir uns diese Eigenschaft?
Mittels dieser Strahlung, die offensichtlich im Radiobereich liegt, ist es möglich, sehr genaue Geschwindigkeitsprofile zu erstellen, die dann mit theoretisch berechneten Rotationskurven mit verschiedener zugrunde liegender Massenverteilung verglichen werden können, wodurch eine Bestimmung der Massenverteilung in unserer Galaxie möglich ist. Da diese Massenverteilung nicht den klassischen Erwartungen entspricht (wie Sie zum Ende des Versuchs sehen werden), sondern zu viel Masse in den äußeren Regionen der galaktischen Scheibe anzeigt, die nicht durch Sterne oder andere herkömmliche Objekte verursacht werden kann, wäre eine neue, nicht leuchtende Form von Materie eine gute Annahme zur Erklärung des Rotationsverlaufes.
Informieren Sie sich über die (bisher bekannten) Eigenschaften der Dunklen Materie, beispielsweise im Carroll & Ostlie oder hier.
Grundlagen
Theorie
Wie entsteht die 21 cm Strahlung?
Schon 1944 wurde von van de Hulst die Existenz einer Emissionslinie des neutralen Wasserstoffs im Radiobereich vorhergesagt. Diese beruht darauf, dass die zwei Spinzustände eines H-Atoms (die Spins von Proton und Elektron können entweder parallel oder antiparallel ausgerichtet sein) etwas unterschiedliche Energien (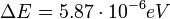 ) aufweisen.
) aufweisen.
Sind beide Spins zu Beginn parallel und klappt dann der Spin des Elektrons um, so wird diese Energiedifferenz in Form eines Photons mit der Wellenlänge von 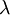 = 21.049 cm abgegeben. Da dies im Radiobereich liegt, ist die mittlere freie Weglänge dieser Photonen sehr groß, sodass sie von nahezu jedem Punkt zu uns dringen können.
= 21.049 cm abgegeben. Da dies im Radiobereich liegt, ist die mittlere freie Weglänge dieser Photonen sehr groß, sodass sie von nahezu jedem Punkt zu uns dringen können.
Allerdings ist dieser übergang nach den quantenmechanischen Auswahlregeln verboten, da sich nur die Spinquantenzahl 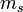 ändert, nicht aber die Bahndrehimpulsquantenzahl l, wie es von der Theorie für einen Dipolübergang (also einen übergang unter Emission eines Photons) gefordert wird. Daher ist die Lebensdauer eines solchen Hyperfeinstrukturzustandes enorm groß; sie liegt bei ca. elf Millionen Jahren. Doch sind im Universum die Dichten der H I-Regionen so gering und die Menge des potentiell strahlenden Wasserstoffs so groß, dass trotz einer mittleren Stoßzeit (nach der der Spinzustand ebenfalls abgeregt ist) von nur 400 Jahren trotzdem genügend solcher verbotenen übergänge stattfinden, um eine starke, den ganzen Himmel erfüllende Strahlung zu messen. Dies geschieht an nahezu allen großen Radioteleskopen und hat sich zu einem eigenen Zweig der Radioastronomie entwickelt.
ändert, nicht aber die Bahndrehimpulsquantenzahl l, wie es von der Theorie für einen Dipolübergang (also einen übergang unter Emission eines Photons) gefordert wird. Daher ist die Lebensdauer eines solchen Hyperfeinstrukturzustandes enorm groß; sie liegt bei ca. elf Millionen Jahren. Doch sind im Universum die Dichten der H I-Regionen so gering und die Menge des potentiell strahlenden Wasserstoffs so groß, dass trotz einer mittleren Stoßzeit (nach der der Spinzustand ebenfalls abgeregt ist) von nur 400 Jahren trotzdem genügend solcher verbotenen übergänge stattfinden, um eine starke, den ganzen Himmel erfüllende Strahlung zu messen. Dies geschieht an nahezu allen großen Radioteleskopen und hat sich zu einem eigenen Zweig der Radioastronomie entwickelt.
Wie viel Wasserstoff gibt es überhaupt im Universum (Stichwort: Nukleosynthese) und warum liegt er größtenteils atomar vor, nicht molekular wie auf der Erde?
Wie rotiert eine Galaxie?
Welche Arten von Galaxien gibt es und wodurch werden sie unterschieden?
Mit Rotation haben Sie sich bestimmt schon oft beschäftigt, zumindest mit der eines starren Körpers. Diese war dadurch gekennzeichnet, dass jeder Massepunkt mit jedem anderen starr verbunden ist, sodass sich der starre Körper mit einer konstanten Winkelgeschwindigkeit 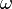 bewegt, für die Bahngeschwindigkeit
bewegt, für die Bahngeschwindigkeit 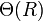 (Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie,
(Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie, 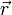 dagegen einen beliebigen Ortsvektor.) also gilt:
dagegen einen beliebigen Ortsvektor.) also gilt:
Etwas anders sieht das Verhalten von 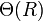 für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte
für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte 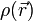 aufweisen. Für ein beliebiges
aufweisen. Für ein beliebiges 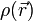 gilt in einem Gravitationspotential
gilt in einem Gravitationspotential 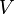 unter Ausnutzung des Virialsatzes (
unter Ausnutzung des Virialsatzes (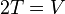 ) die Beziehung:
) die Beziehung:
Dabei steht 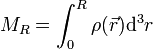 für die innerhalb des Radius
für die innerhalb des Radius 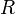 eingeschlossene Masse. Diese Abhängigkeit
eingeschlossene Masse. Diese Abhängigkeit 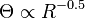 wird auch als Kepler-Rotation bezeichnet, sie beschreibt die Rotation von gravitativ gebundenen kleinen Objekten um eine große Zentralmasse (Planetensystem!). Setzen wir uns auf einen festen Radius innerhalb der Scheibe der Milchstraße, ist
wird auch als Kepler-Rotation bezeichnet, sie beschreibt die Rotation von gravitativ gebundenen kleinen Objekten um eine große Zentralmasse (Planetensystem!). Setzen wir uns auf einen festen Radius innerhalb der Scheibe der Milchstraße, ist 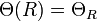 also konstant, so folgt für die Massendichte:
also konstant, so folgt für die Massendichte:
Durch eine Messung der der Rotationskurve 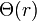 kann somit direkt auf die Massenverteilung in einer Galaxie rückgeschlossen werden.
kann somit direkt auf die Massenverteilung in einer Galaxie rückgeschlossen werden.
Machen Sie sich die Verläufe der Rotationskurven unter Annahme einer starren Körper- oder Kepler-Rotation auch grafisch klar!
Praxis
Ziel ist es also, die Massenverteilung 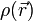 innerhalb unserer Galaxie (besser: der Scheibe unserer Galaxie) durch die Messung der Rotationsgeschwindigkeit
innerhalb unserer Galaxie (besser: der Scheibe unserer Galaxie) durch die Messung der Rotationsgeschwindigkeit 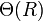 zu bestimmen. Dies bringt allerdings das große Problem mit sich, dass sich auch unsere Sonne und somit die Erde um das galaktische Zentrum herum bewegt. Eine Messung der Rotationsgeschwindigkeit ist daher immer nur die Messung der Relativgeschwindigkeit zwischen der Erde und dem Objekt, dessen Geschwindigkeit wir gerade vermessen. Glücklicher Weise ist die Geschwindigkeit, mit der sich die Sonne um das galaktische Zentrum bewegt, recht gut bekannt, sodass sie lediglich zu dieser Relativgeschwindigkeit hinzuaddiert werden muss. Ihr Wert beträgt
zu bestimmen. Dies bringt allerdings das große Problem mit sich, dass sich auch unsere Sonne und somit die Erde um das galaktische Zentrum herum bewegt. Eine Messung der Rotationsgeschwindigkeit ist daher immer nur die Messung der Relativgeschwindigkeit zwischen der Erde und dem Objekt, dessen Geschwindigkeit wir gerade vermessen. Glücklicher Weise ist die Geschwindigkeit, mit der sich die Sonne um das galaktische Zentrum bewegt, recht gut bekannt, sodass sie lediglich zu dieser Relativgeschwindigkeit hinzuaddiert werden muss. Ihr Wert beträgt 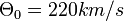 nach dem aktuellen Standardwert der IAU. Ihre Bestimmung beruht auf der Messung der sog. Pekuliargeschwindigkeiten vieler verschiedener Sterne der Galaxie und soll hier nicht weiter diskutiert werden.
nach dem aktuellen Standardwert der IAU. Ihre Bestimmung beruht auf der Messung der sog. Pekuliargeschwindigkeiten vieler verschiedener Sterne der Galaxie und soll hier nicht weiter diskutiert werden.
Wie kommt man nun aber an die Relativgeschwindigkeit zwischen uns und einem Punkt bei einem beliebigen galaktozentrischen Radius 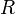 ? Dabei hilft der wohl bekannte Doppler-Effekt, der an vielen Stellen in der Astronomie genutzt wird. Eine (stark idealisierte, aber hilfreiche) Annahme ist darüber hinaus, dass die Rotationsgeschwindigkeit vom galaktischen Zentrum nach außen monoton abnimmt.
? Dabei hilft der wohl bekannte Doppler-Effekt, der an vielen Stellen in der Astronomie genutzt wird. Eine (stark idealisierte, aber hilfreiche) Annahme ist darüber hinaus, dass die Rotationsgeschwindigkeit vom galaktischen Zentrum nach außen monoton abnimmt.
Informieren Sie sich über das galaktische Koordinatensystem, das in diesem Versuch sehr hilfreich ist und Sie daher für die Steuerung des Teleskops unbedingt benötigen!
Betrachten wir die Scheibe der Milchstraße (galaktische Breite 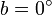 ) unter einem Winkel
) unter einem Winkel 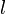 (der galaktischen Länge) und messen die Strahlung des neutralen Wasserstoffs auf diesem Sehstrahl, so erhalten wir beispielsweise ein Spektrum, wie es in Bild 2 zu sehen ist. Da sich die H I-Regionen A, B, C, D mit unterschiedlicher Geschwindigkeit bewegen, sind ihre 21 cm-Emissionslinien unterschiedlich stark Doppler-verschoben. Der Radialanteil der Geschwindigkeit (also die Geschwindigkeit, mit der sich eine Wolke auf uns zu oder von uns weg bewegt) ist dabei gegeben durch:
(der galaktischen Länge) und messen die Strahlung des neutralen Wasserstoffs auf diesem Sehstrahl, so erhalten wir beispielsweise ein Spektrum, wie es in Bild 2 zu sehen ist. Da sich die H I-Regionen A, B, C, D mit unterschiedlicher Geschwindigkeit bewegen, sind ihre 21 cm-Emissionslinien unterschiedlich stark Doppler-verschoben. Der Radialanteil der Geschwindigkeit (also die Geschwindigkeit, mit der sich eine Wolke auf uns zu oder von uns weg bewegt) ist dabei gegeben durch:
Dabei bezeichnet c die Vakuumlichtgeschwindigkeit, 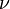 die gemessene Frequenz und
die gemessene Frequenz und 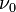 die Laborfrequenz der 21 cm H I-Linie. Wie man sich leicht überlegen kann, ist die größte Doppler-Geschwindigkeit
die Laborfrequenz der 21 cm H I-Linie. Wie man sich leicht überlegen kann, ist die größte Doppler-Geschwindigkeit 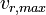 stets die, die zu der Region mit dem kleinsten galaktozentrischen Radius
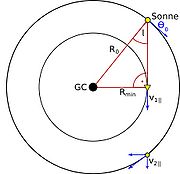
stets die, die zu der Region mit dem kleinsten galaktozentrischen Radius 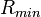 gehört (Dazu die oben erwähnte Annahme!). Durch eine einfache trigonometrische Betrachtung folgt sofort
gehört (Dazu die oben erwähnte Annahme!). Durch eine einfache trigonometrische Betrachtung folgt sofort 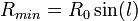 , wobei
, wobei 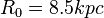 den Abstand der Sonne vom galaktischen Zentrum bezeichnet.
den Abstand der Sonne vom galaktischen Zentrum bezeichnet.
Um nun die Rotationsgeschwindigkeit 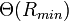 zu bestimmen, muss noch die Eigenbewegung der Sonne berücksichtigt werden. Ihre Komponente in Richtung des Sehstrahls ist, wie man ebenfalls geometrisch begründen kann,
zu bestimmen, muss noch die Eigenbewegung der Sonne berücksichtigt werden. Ihre Komponente in Richtung des Sehstrahls ist, wie man ebenfalls geometrisch begründen kann, 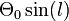 . Damit folgt
. Damit folgt 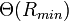 zu:
zu:
Die so ermittelte Rotationsgeschwindigkeit 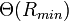 muss allerdings noch einer Korrektur unterzogen werden, da die bisherige Ableitung auf der Annahme beruht, dass sich unser Sonnensystem auf einer perfekten Kreisbahn um das galaktische Zentrum bewegt. Dies ist natürlich nicht der Fall (warum?), sodass eine Korrektur für den sog. Local Standard of Rest (LSR) durchgeführt werden muss. Der LSR ist ein hypothetischer Punkt, der eine genaue Kreisbahn um das galaktische Zentrum beschreibt und einen Radius hat, der genau der mittleren Entfernung Sonne -- galaktisches Zentrum entspricht. Da die Sonne sich eben nicht auf einer exakt Kreisbahn bewegt, hat sie stets eine Relativgeschwindigkeit zum LSR, für die korrigiert werden muss. Die Berechnung von
muss allerdings noch einer Korrektur unterzogen werden, da die bisherige Ableitung auf der Annahme beruht, dass sich unser Sonnensystem auf einer perfekten Kreisbahn um das galaktische Zentrum bewegt. Dies ist natürlich nicht der Fall (warum?), sodass eine Korrektur für den sog. Local Standard of Rest (LSR) durchgeführt werden muss. Der LSR ist ein hypothetischer Punkt, der eine genaue Kreisbahn um das galaktische Zentrum beschreibt und einen Radius hat, der genau der mittleren Entfernung Sonne -- galaktisches Zentrum entspricht. Da die Sonne sich eben nicht auf einer exakt Kreisbahn bewegt, hat sie stets eine Relativgeschwindigkeit zum LSR, für die korrigiert werden muss. Die Berechnung von 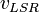 ist recht kompliziert, da eine Vielzahl an Korrekturgrößen berücksichtigt werden müssen. Für den täglichen Gebrauch haben sich daher kleine Programme etabliert, die eine komfortable Berechnung ermöglichen (z. B. http://www.jupiterspacestation.org/software/Vlsr.html). Die LSR-korrigierte Rotationsgeschwindigkeit ist dann schlicht:
ist recht kompliziert, da eine Vielzahl an Korrekturgrößen berücksichtigt werden müssen. Für den täglichen Gebrauch haben sich daher kleine Programme etabliert, die eine komfortable Berechnung ermöglichen (z. B. http://www.jupiterspacestation.org/software/Vlsr.html). Die LSR-korrigierte Rotationsgeschwindigkeit ist dann schlicht:
Machen Sie sich diesen Zusammenhang auch anhand von Carroll & Ostlie, Kapitel 24.3, klar! Wieso kann nur der Peak bei der maximalen Doppler-Verschiebung zur Geschwindigkeitsbestimmung genutzt werden? Bei welchem 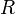 liegt also das Limit dieser Methode?
liegt also das Limit dieser Methode?
Der Versuch
Außer des wissenschaftlichen Ziels Vermessung der Rotationseigenschaften der Milchstraße verfolgt der Versuch natürlich auch Absicht, Ihnen einen Eindruck von der Arbeit mit einem Radioteleskop zu vermitteln (Die Ruhr-Universität-Bochum ist immerhin die einzige Uni Deutschlands, die das anbieten kann!). Daher folgt nun ein kurzer Überblick über das am AIRUB zur Verfügung stehende Radioteleskop.
Das Teleskop
Das Radioteleskop befindet sich auf dem Dach des Gebäudes NA in einer für Radiowellen durchsichtigen Kuppel, die das Teleskop, seine Elektronik und nicht zuletzt Sie selbst vor Wind und Wetter schützt. Dort wird sich also auch der Versuch abspielen. Der Durchmesser der Schüssel, die von einer alten Richtfunkstrecke stammt, beträgt 3 m; ist verglichen mit den großen Observatorien der Welt also sehr klein. Da die Winkelauflösung eines optischen Instruments 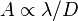 ist, wobei
ist, wobei 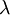 die beobachtete Wellenlänge und
die beobachtete Wellenlänge und 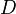 den Durchmesser der Apertur bezeichnet, ist die minimal mögliche räumliche Auflösung recht groß. Dies bringt allerdings auch einen Vorteil mit sich, denn der Beam (also der Bereich, in dem das Teleskop Daten sammelt) ist mit
den Durchmesser der Apertur bezeichnet, ist die minimal mögliche räumliche Auflösung recht groß. Dies bringt allerdings auch einen Vorteil mit sich, denn der Beam (also der Bereich, in dem das Teleskop Daten sammelt) ist mit 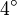 ebenfalls sehr groß, sodass geringe Fehler beim Pointing oder der Nachführung nicht ins Gewicht fallen.
ebenfalls sehr groß, sodass geringe Fehler beim Pointing oder der Nachführung nicht ins Gewicht fallen.
Die spektrale Auflösung beträgt 37.5 kHz, was einer Doppler-Geschwindigkeit von ca. 8 km/s entspricht. Mit dem 2 MHz Detektor kann so ein Geschwindigkeitsbereich von nahezu 500 km/s abgedeckt werden. Da das 21 cm Signal des neutralen Wasserstoffs unpolarisiert ist, muss auf eine Polarisation keine Rücksicht genommen werden.
Warum ist die H I-Linie unpolarisiert bzw. wie kommt Polarisation in der Astronomie häufig zustande?
Ebenfalls ein Vorteil der geringen Größe ist die Schnelligkeit der Positionierung. Diese geschieht durch zwei Schrittmotoren, die das Teleskop mit bis zu 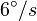 bewegen können. Dadurch ergibt sich die sehr geringe Zenitblindheit (Als Zenitblindheit wird ein Fehler im Nachführungsalgorithmus horizontal montierter Teleskope bezeichnet. Dieser sorgt dafür, dass im Moment des Zenitdurchgangs eines Objekts, auf das gerade getrackt wird, die Nachführungsgeschwindigkeit unendlich groß wird.) von unter einem Grad. Da durch die geringe Sammelfläche des Teleskops längere Integrationszeiten notwendig sein könnten, ist dies recht praktisch.
bewegen können. Dadurch ergibt sich die sehr geringe Zenitblindheit (Als Zenitblindheit wird ein Fehler im Nachführungsalgorithmus horizontal montierter Teleskope bezeichnet. Dieser sorgt dafür, dass im Moment des Zenitdurchgangs eines Objekts, auf das gerade getrackt wird, die Nachführungsgeschwindigkeit unendlich groß wird.) von unter einem Grad. Da durch die geringe Sammelfläche des Teleskops längere Integrationszeiten notwendig sein könnten, ist dies recht praktisch.
Informieren Sie sich bei Wilson, Rohlfs & Hüttemeister über grundlegende Parameter der Radioastronomie wie das Signal zu Rauschen Verhältnis und dessen Abhängigkeit von der Integrationszeit.
Gesteuert werden sowohl das Teleskop selbst als das Spektrometer, welches die ankommende Strahlung misst, mit einem Laptop, an den beide Geräte über eine serielle Schnittstelle angebunden werden. Die Steuerungssoftware stellt alle wichtigen Bedienmöglichkeiten in einer grafischen Benutzungsoberfläche zur Verfügung; im Versuch werden Sie jedoch hauptsächlich die Eingabefelder für eine Positionierung und die Aufnahme eines Spektrums benötigen. Trotzdem sind Sie dazu eingeladen, alle Befehle einmal auszuprobieren, um einen Eindruck von der Arbeit mit einem computergesteuerten Teleskop zu bekommen. Dabei sind selbstverständlich entsprechende Sicherungsmechanismen aktiv, die eine mechanische Beschädigung des Teleskops vermeiden sollen, da die Motoren eine enorme Kraft aufbringen können. Daher sollten Sie stets aufpassen, wohin sich das Teleskop gerade bewegt, insbesondere bei neuen Positionierungen, denn die Kuppel ist nicht sehr geräumig.
Die Betriebsanleitung für das AIRUB Radioteleskop finden Sie zum Download im Literaturverzeichnis. Um den Versuch erfolgreich durchführen zu können, ist eine gründliche Lektüre unabdingbar!
Messaufgaben
Um nun die Rotationskurve unserer Galaxie zu bestimmen, vermessen Sie die maximalen Radialgeschwindigkeiten in Abhängigkeit von der galaktischen Länge innerhalb der Scheibe der Milchstraße. Diese Messung geschieht in zwei Winkelbereichen, einmal 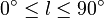 und
und 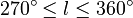 , beide Messreihen in
, beide Messreihen in 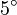 -Schritten. Mit der ersten Messung schauen Sie also in den linken Teil der Milchstraße (vom galaktischen Nordpol aus betrachtet), mit der zweiten Messung in den rechten Teil. Die Wahl der Integrationszeit sowie der anderen Beobachtungsparameter ist dabei Ihnen überlassen. Bitte beachten Sie, dass je nach Jahreszeit ggf. nur ein Teil der
Milchstraße beobachtbar sein könnte!
Um eine direkte Kontrolle zu haben, ob sinnvolle Ergebnisse dabei heraus kommen, sollten Sie mittels der Spektren-Vorschau innerhalb der Steuerungssoftware schon während des Versuchs eine erste, frei-Hand Rotationskurve erstellen!
-Schritten. Mit der ersten Messung schauen Sie also in den linken Teil der Milchstraße (vom galaktischen Nordpol aus betrachtet), mit der zweiten Messung in den rechten Teil. Die Wahl der Integrationszeit sowie der anderen Beobachtungsparameter ist dabei Ihnen überlassen. Bitte beachten Sie, dass je nach Jahreszeit ggf. nur ein Teil der
Milchstraße beobachtbar sein könnte!
Um eine direkte Kontrolle zu haben, ob sinnvolle Ergebnisse dabei heraus kommen, sollten Sie mittels der Spektren-Vorschau innerhalb der Steuerungssoftware schon während des Versuchs eine erste, frei-Hand Rotationskurve erstellen!
Zur Fehlerbetrachtung: Berücksichtigen Sie sowohl die Größe des Beams als Maß für die Unsicherheit der galaktischen Position als auch die Auflösung des Spektrometers für die Unsicherheit der gemessenen Geschwindigkeiten. Da die Messungen in Regionen 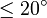 Abstand vom galaktischen Zentrum und zu
Abstand vom galaktischen Zentrum und zu 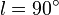 bzw.
bzw. 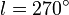 hin schwierig werden, sollten Sie hier größere Fehler annehmen.
hin schwierig werden, sollten Sie hier größere Fehler annehmen.
Um zusätzlich noch einen Eindruck von der Dicke der Scheibe der Milchstraße zu bekommen, fahren Sie das Teleskop anschließend auch zu galaktischen Breiten, die von 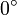 verschieden sind. Tun Sie dies bei mindestens drei verschiedenen Längen. Bis zu welchen Breiten können Sie noch Wasserstoff detektieren? Welcher Dicke entspricht dieser Winkel?
verschieden sind. Tun Sie dies bei mindestens drei verschiedenen Längen. Bis zu welchen Breiten können Sie noch Wasserstoff detektieren? Welcher Dicke entspricht dieser Winkel?
Auswertung
Für die genaue Auswertung speichern Sie die erhobenen Spektraldaten in einer Datei ab, die Sie am Ende des Versuchs zur Auswertung mitnehmen. Aufgrund dieser Daten erstellen Sie die Rotationskurve unserer Galaxie mit den entsprechenden Fehlerbalken. Dazu ist ein wissenschaftliches Datenverarbeitungsprogramm wie Origin oder das kostenlose QtiPlot empfehlenswert, das sie auf den Seiten des F-Praktikums herunterladen können.
Welche Art von Rotation liegt also vor bzw. worin unterscheidet sich die Rotationskurve unserer Galaxie von den oben diskutierten Verläufen? Versuchen Sie, eine Beziehung für die Massendichte 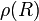 zu finden, die zu ihrem Messergebnis passt (hilfreich dazu ist wiederum ein Blick in Carroll & Ostlie und die Verwendung eines Programms wie Maple). Vergleichen Sie zum Schluss diese Massendichte mit der bei Sternzählungen gefundenen Verteilung, die einen Abfall der Sterndichte mit
zu finden, die zu ihrem Messergebnis passt (hilfreich dazu ist wiederum ein Blick in Carroll & Ostlie und die Verwendung eines Programms wie Maple). Vergleichen Sie zum Schluss diese Massendichte mit der bei Sternzählungen gefundenen Verteilung, die einen Abfall der Sterndichte mit 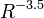 anzeigt. Wie würden Sie die Diskrepanz erklären?
anzeigt. Wie würden Sie die Diskrepanz erklären?
Allgemeiner Hinweis: Diese Anleitung versteht sich nicht als halbes Lehrbuch, ein Blick in die angegebene Literatur ist daher äußerst (!) ratsam. Die fett gedruckten Fragen im Text sollen Ihnen dabei eine Orientierung geben und stecken in etwa den Inhalt des Vorgesprächs ab. Dieses versteht sich ebenfalls nicht als halbe Prüfung, sondern als Vorbereitung im wörtlichen Sinne.
Literatur
Die angegebene Literatur finden Sie sowohl in der Bibliothek der Fakultät für Physik und Astronomie (NB 1/Süd), der Langzeitausleiher, als auch in der Bibliothek des Astronomischen Instituts (AIRUN) (NA 7/Nord). In der Bibliothek des AIRUB finden Sie auch erheblich weiterführende Literatur. Bitte kontaktieren Sie ihren Betreuer für Zugang und Nutzung der Bibliothek des Astronomischen Instituts (NA 7/Nord).
- Carroll, Bradley W. & Ostlie, Dale A.: An Introduction to Modern Astrophysics, 2nd edition, 2007, Addison Wesley Publishers
- Wilson, Thomas L. & Rohlfs, Kristen & Hüttemeister, Susanne: Tools of Radio Astronomy, 5th edn., 2009, Springer-Verlag Berlin Heidelberg
- Roos, Matts: Dark Matter: The evidence from astronomy, astrophysics and cosmology, 2010, http://arxiv.org/abs/1001.0316
- Betriebsanleitung des AIRUB Radioteleskops
Bomans 17:40 31.08.2017
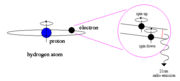
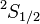 von F=1 nach F=0, der die Emission eines Photons mit der Frequenz
von F=1 nach F=0, der die Emission eines Photons mit der Frequenz 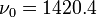 GHz zur Folge hat. Rechts: Das Termschema des Wasserstoffs mit den entsprechenden Hyperfeinstrukturniveaus.
GHz zur Folge hat. Rechts: Das Termschema des Wasserstoffs mit den entsprechenden Hyperfeinstrukturniveaus.