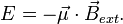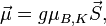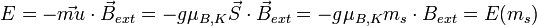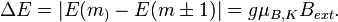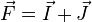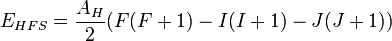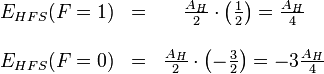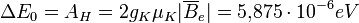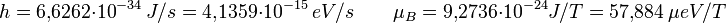Hyperfeinstruktur in der ESR: Unterschied zwischen den Versionen
| Zeile 54: | Zeile 54: | ||
=== HFS-Niveaus in externen Magnetfeldern === | === HFS-Niveaus in externen Magnetfeldern === | ||
| − | + | Mit einem externen Magnetfeld wird die Entartung bezüglich der z-Komponente von F aufgehoben. | |
== Übungsaufgaben == | == Übungsaufgaben == | ||
Version vom 22. Mai 2012, 12:59 Uhr
Dieser Versuch beschäftigt sich mit der Messung des Intervallfaktors in der Hyperfeinstruktur des atomaren Wasserstoffs. Dieser Faktor gibt die Wechselwirkung zwischen dem ungepaarten S-Elektron und dem Kernspin wieder und führt zu einer Aufhebung der Entartung bezüglich der beiden möglichen Spineinstellungen des Elektron- und Kernspins (parallel oder anti-parallel). Die Energiedifferenz, die mit dieser Aufspaltung verbunden ist, entspricht der bekannten 21 cm-Linie (1420 MHz) des Wasserstoffs. Jedoch wird in diesem Versuch kein atomares Wasserstoffgas benutzt, sondern separierte Wasserstoffatome, die in einer gefrorenen Ammoniak-Matrix eingebettet sind. Des weiteren wird die Breit-Rabi-Formel für unseren Fall experimentell nachgewiesen.
Inhaltsverzeichnis
Vorbemerkungen
Der Versuch findet im Labor der Arbeitsgruppe I (Polarisiertes Target) im Institut für Experimentalphysik I NB 05/496-497 statt.
Da die Versuchsdurchführung unkompliziert in relativ kurzer Zeit durchführbar ist und auch die häusliche Auswertung nicht sonderlich aufwendig sein wird, besteht ein Hauptaufgabenteil aus einer guten und soliden Vorbereitung der theoretischen Grundlagen zu den behandelten Phänomenen.
Diese Seite gibt nur eine kurze Zusammenfassung der Anleitung wieder.
Zur Theorie der HFS
Ein Teilchen im Magnetfeld
Wird ein magnetisches Moment 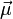 einem externen Magnetfeld
einem externen Magnetfeld 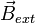 ausgesetzt, so besitzt es in diesem die Energie
ausgesetzt, so besitzt es in diesem die Energie
Geladene Elementarteilchen besitzen, sofern sie einen von Null verschiedenen Eigendrehimpuls (Spin 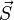 ) haben, ein magnetisches Moment
) haben, ein magnetisches Moment
welches in analoger Weise mit einem äußeren Magnetfeld wechselwirkt. Man definiert den g-Faktor als denjenigen Faktor, um den das magnetische Moment des Teilchens vom Wert des entsprechenden "klassischen Kreisstroms" abweicht. Letzterer wird als Magneton bezeichnet. Es sei 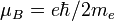 das sogenannte Bohr'sche Magneton sowie
das sogenannte Bohr'sche Magneton sowie 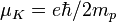 das Kernmagneton mit der Elektronen- bzw. Protonenmasse me und mp. Ein weiterer Unterschied zum klassischen Fall des Kreisstroms ergibt sich aus der Quantisierung des Eigendrehimpulses.
Ist
das Kernmagneton mit der Elektronen- bzw. Protonenmasse me und mp. Ein weiterer Unterschied zum klassischen Fall des Kreisstroms ergibt sich aus der Quantisierung des Eigendrehimpulses.
Ist 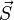 der Spin des Teilchens, so kann dessen Projektion bezüglich einer bestimmten Vorzugsrichtung
der Spin des Teilchens, so kann dessen Projektion bezüglich einer bestimmten Vorzugsrichtung 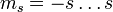 insgesamt 2s+1 verschiedene Werte annehmen. Der Wert der ms (magnetische Quantenzahl) ändert sich dabei immer nur um eine Einheit. Damit schreibt sich die Energie zu
insgesamt 2s+1 verschiedene Werte annehmen. Der Wert der ms (magnetische Quantenzahl) ändert sich dabei immer nur um eine Einheit. Damit schreibt sich die Energie zu
Nach den quantenmechanischen Auswahlregeln darf sich bei einem Übergang die magnetische Quantenzahl nur um eine Einheit ändern. Die bei einem Übergang aufgenommene bzw. abgegebene Energiemenge ist also
siehe hierzu Übung 1
Aufspaltung der Energieniveaus
In diesem Versuch beschäftigen wir uns mit den verschiedenen Formen der Energieniveau-Aufspaltungen. Wie wir schon beim Anlegen eines äußeren Felds gesehen haben, gibt es eine Aufspaltung der Energieniveaus bezüglich der magnetischen Quantenzahlen.
Jedoch findet auch im Nullfeld eine Aufspaltung des Wasserstoffgrundzustandes (WGZ) statt. Hierbei koppelt der Kernspin 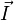 mit dem Hüllenspin
mit dem Hüllenspin 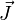 zu einem neuen Gesamtdrehimpuls
zu einem neuen Gesamtdrehimpuls
mit mF=-F,-F+1,...,F.
Für den WGZ können nur zwei Werte auftreten und zwar 0 und 1 für eine anti-parallele oder eine parallele Stellung der jeweiligen Spins. Aus der Beziehung
mit 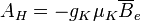 lassen sich die Energien der beiden Einstellungsmöglichkeiten bestimmen (I=J=1/2)
lassen sich die Energien der beiden Einstellungsmöglichkeiten bestimmen (I=J=1/2)
Bestimmt man das wirkende Magnetfeld am Ort des Kerns 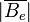 , welches vom Elektron erzeugt wird, so erhält man für AH:
, welches vom Elektron erzeugt wird, so erhält man für AH:
HFS-Niveaus in externen Magnetfeldern
Mit einem externen Magnetfeld wird die Entartung bezüglich der z-Komponente von F aufgehoben.
Übungsaufgaben
Übung 1
Wie viele Energieniveaus besitzt ein freies Elektron 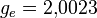 ) und welche Übergangsfrequenz hat es in einem äußeren Magnetfeld der Stärke Bext=0,335 T?
) und welche Übergangsfrequenz hat es in einem äußeren Magnetfeld der Stärke Bext=0,335 T?
Vorzubereitende Themen
a) klassische und quantenmechanische Beschreibung des Drehimpulses, Spin
b) magnetisches Moment, g-Faktor, Energie eines magnetischen Moments im äußeren Magnetfeld
c) atomare Fein- und Hyperfeinstruktur-Wechselwirkung
d) Zeeman-Effekt, Paschen-Back-Effekt, Breit-Rabi-Formel
e) Grundlagen eines Elektronenspin-Resonanzspektrometers
Literatur
T. Mayer-Kuckuk 'Atomphysik' T. Mayer-Kuckuk 'Kernphysik' Bergmann-Schaefer 'Experimentalphysik Bd IV Teil 1+2' Jedes einführende Lehrbuch zur Festkörperphysik bezgl. der ESR-Apparatur möglicherweise Angabe aus Biophysik-ESR-Versuch
Kontakt: Dr. Gerhard Reicherz reicherz@ep1.rub.de, Tel. 23542, NB 2/127
Anleitung: PDF