Dunkle Materie in der Milchstraße?: Unterschied zwischen den Versionen
Zinn (Diskussion | Beiträge) |
Zinn (Diskussion | Beiträge) |
||
| Zeile 40: | Zeile 40: | ||
Mit Rotation haben Sie sich bestimmt schon oft beschäftigt, zumindest mit der eines starren Körpers. Diese war dadurch gekennzeichnet, dass jeder Massepunkt mit jedem anderen starr verbunden ist, sodass sich der starre Körper mit einer konstanten Winkelgeschwindigkeit <math>\omega</math> bewegt, für die Bahngeschwindigkeit <math>\Theta(R)</math> (Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie, <math>\vec{r}</math> dagegen einen beliebigen Ortsvektor.) also gilt: | Mit Rotation haben Sie sich bestimmt schon oft beschäftigt, zumindest mit der eines starren Körpers. Diese war dadurch gekennzeichnet, dass jeder Massepunkt mit jedem anderen starr verbunden ist, sodass sich der starre Körper mit einer konstanten Winkelgeschwindigkeit <math>\omega</math> bewegt, für die Bahngeschwindigkeit <math>\Theta(R)</math> (Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie, <math>\vec{r}</math> dagegen einen beliebigen Ortsvektor.) also gilt: | ||
| − | <math>\Theta = \omega R</math> | + | |
| + | :<math>\Theta = \omega R</math> | ||
| + | |||
Etwas anders sieht das Verhalten von <math>\Theta (R)</math> für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte <math>\rho(\vec{r})</math> aufweisen. Für ein beliebiges <math>\rho(\vec{r})</math> gilt in einem Gravitationspotential <math>V</math> unter Ausnutzung des Virialsatzes (2T = V) die Beziehung: | Etwas anders sieht das Verhalten von <math>\Theta (R)</math> für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte <math>\rho(\vec{r})</math> aufweisen. Für ein beliebiges <math>\rho(\vec{r})</math> gilt in einem Gravitationspotential <math>V</math> unter Ausnutzung des Virialsatzes (2T = V) die Beziehung: | ||
Version vom 22. März 2012, 14:46 Uhr
Die Existenz Dunkler Materie gilt als eines der großen Rätsel moderner Astronomie und Physik. Diese seltsame Form von Materie macht sich ausschließlich durch ihre gravitative Wechselwirkung bemerkbar und entzieht sich bislang der direkten Beobachtung mit konventionellen Teleskopen oder in Beschleuniger-Experimenten. Ihre gravitative Wechselwirkung ist jedoch erstaunlich einfach zu beobachten, was in diesem Versuch, der im Übrigen genau so vor ca. 40 Jahren zum Postulat Dunkler Materie geführt hat, geschehen soll. Mit dem 3m-Radioteleskop des Astronomischen Instituts auf dem Dach des NA-Gebäudes kann der Hyperfeinstruktur-Übergang des neutralen Wasserstoffs in der Milchstraße gemessen und aus dessen Verteilung auf fehlende - daher "dunkle" - Materie geschlossen werden, die nötig ist, um die Beobachtungen zu erklären. Im Versuch werden die folgenden Aspekte angegangen:
- Umgang mit einem motorisierten und computergesteuerten Teleskop
- charakteristische Größen eines Teleskops (Empfindlichkeit, Auflösungsvermögen)
- Planung und Durchführung eines geeigneten Messprogramms
- stat. Datenauswertung
WICHTIG: Vor der Buchung dieses Versuchs sollte unbedingt eine Terminabsprache per Mail erfolgen (zinn@astro.rub.de), da die Milchstraße zum gewünschten Termin schließlich auch hoch am Himmel stehen muss.
Inhaltsverzeichnis
Einleitung
Von Dunkler Materie hat wohl Jeder schon einmal etwas gehört. Versteckt, geheimnisvoll, eben völlig dunkel soll sie unser Universum erfüllen und dort für einen großen Teil der Gravitation sorgen. Ohne sie wäre es überhaupt nicht so schnell zur Bildung von Sternen, Galaxien und Haufen gekommen, sodass wir alle heute nicht existieren würden, sagen uns die Kosmologen. Nicht so glücklich mit ihr sind hingegen die Teilchenphysiker, deren größte Aufgabe es zur Zeit ist, ihr endlich das dunkle zu nehmen und ein Elementarteilchen zu präsentieren, aus dem sie besteht.
Fest steht nur (mit nahezu absoluter Sicherheit), dass es Dunkle Materie wirklich gibt. Dafür sprechen zahlreiche Messungen und auch theoretische überlegungen zur Dunklen Materie vor allem im frühen Universum. Doch was sind das für Messungen? Kann man sie überhaupt nachvollziehen, sodass sich jeder (mit relativ gerigem Aufwand) von den Ergebnissen überzeugen kann? Diese Fragen sollen mit diesem Versuch zumindest teilweise geklärt werden, indem genau die Messung nachempfunden wird, die zum Postulieren von Dunkler Materie geführt hat: Die Vermessung der Rotationsgeschwindigkeit(en) von Galaxien.
Die erste Galaxie, die es sich lohnt, zu untersuchen, ist natürlich unsere eigene, die Milchstraße. Darüber hinaus bietet sie sich auch an, weil wir uns direkt in ihr befinden, ihre Strahlung sollte also die stärkste und damit leicht zu beobachten sein. Die grundsätzliche Vorgehensweise ist jedoch auch bei externen Galaxien nicht anders, jedoch muss hier erheblich mehr Aufwand getrieben werden.
Bleibt nur noch die Frage, welche Art von Strahlung sich am besten zur Ableitung einer Rotationskurve (Rotationsgeschwindigkeit aufgetragen gegen die Entfernung vom galaktischen Zentrum) eignet. Sie müsste idealer Weise über die gesamte Ausdehnung der Milchstraße sichtbar sein, sodass von jedem Ort Daten erhoben werden können. Messungen im optischen Wellenlängenbereich scheiden also schon einmal aus, genau so wie noch kurzwelligere Strahlung. Doch die Natur meint es gut mit den Astronomen, denn sie hat das ideale Werkzeug für unsere Anforderungen bereit gestellt: die 21 cm Strahlung von neutralem Wasserstoff, auch H I genannt.
Warum ist gerade diese 21 cm Strahlung für unsere Beobachtung so geeignet im Vergleich zu anderen Wellenlängen und wodurch ``erkaufen wir uns diese Eigenschaft?
Mittels dieser Strahlung, die offensichtlich im Radiobereich liegt, ist es möglich, sehr genaue Geschwindigkeitsprofile zu erstellen, die dann mit theoretisch berechneten Rotationskurven mit verschiedener zugrunde liegender Massenverteilung verglichen werden können, wodurch eine Bestimmung der Massenverteilung in unserer Galaxie möglich ist. Da diese Massenverteilung nicht den klassischen Erwartungen entspricht (wie Sie zum Ende des Versuchs sehen werden), sondern zu viel Masse in den äußeren Regionen der galktischen Scheibe anzeigt, die nicht durch Sterne oder andere ``herkömmliche Objekte verursacht werden kann, wäre eine neue, nicht leuchtende Form von Materie eine gute Annahme zur Erklärung des Rotationsverlaufes.
Informieren Sie sich über die (bisher bekannten) Eigenschaften der Dunklen Materie, beispielsweise im Carroll & Ostlie oder hier.
Grundlagen
Theorie
Wie entsteht die 21 cm Strahlung?
Schon 1944 wurde von van de Hulst die Existenz einer Emissionslinie des neutralen Wasserstoffs im Radiobereich vorhergesagt. Diese beruht darauf, dass die zwei Spinzustände eines H-Atoms (die Spins von Proton und Elektron können entweder parallel oder antiparallel ausgerichtet sein) etwas unterschiedliche Energien (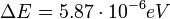 ) aufweisen.
) aufweisen.
Sind beide Spins zu Beginn parallel und klappt dann der Spin des Elektrons um, so wird diese Energiedifferenz in Form eines Photons mit der Wellenlänge von 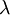 = 21.049 cm abgegeben. Da dies im Radiobereich liegt, ist die mittlere freie Weglänge dieser Photonen sehr groß, sodass sie von nahezu jedem Punkt zu uns dringen können.
= 21.049 cm abgegeben. Da dies im Radiobereich liegt, ist die mittlere freie Weglänge dieser Photonen sehr groß, sodass sie von nahezu jedem Punkt zu uns dringen können.
Allerdings ist dieser übergang nach den quantenmechanischen Auswahlregeln verboten, da sich nur die Spinquantenzahl 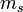 ändert, nicht aber die Bahndrehimpulsquantenzahl l, wie es von der Theorie für einen Dipolübergang (also einen übergang unter Emission eines Photons) gefordert wird. Daher ist die Lebensdauer eines solchen Hyperfeinstrukturzustandes enorm groß; sie liegt bei ca. elf Millionen Jahren. Doch sind im Universum die Dichten der H I-Regionen so gering und die Menge des potentiell strahlenden Wasserstoffs so groß, dass trotz einer mittleren Stoßzeit (nach der der Spinzustand ebenfalls abgeregt ist) von nur 400 Jahren trotzdem genügend solcher verbotenen übergänge stattfinden, um eine starke, den ganzen Himmel erfüllende Strahlung zu messen. Dies geschieht an nahezu allen großen Radioteleskopen und hat sich zu einem eigenen Zweig der Radioastronomie entwickelt.
ändert, nicht aber die Bahndrehimpulsquantenzahl l, wie es von der Theorie für einen Dipolübergang (also einen übergang unter Emission eines Photons) gefordert wird. Daher ist die Lebensdauer eines solchen Hyperfeinstrukturzustandes enorm groß; sie liegt bei ca. elf Millionen Jahren. Doch sind im Universum die Dichten der H I-Regionen so gering und die Menge des potentiell strahlenden Wasserstoffs so groß, dass trotz einer mittleren Stoßzeit (nach der der Spinzustand ebenfalls abgeregt ist) von nur 400 Jahren trotzdem genügend solcher verbotenen übergänge stattfinden, um eine starke, den ganzen Himmel erfüllende Strahlung zu messen. Dies geschieht an nahezu allen großen Radioteleskopen und hat sich zu einem eigenen Zweig der Radioastronomie entwickelt.
Wie viel Wasserstoff gibt es überhaupt im Universum (Stichwort: Nukleosynthese) und warum liegt er größtenteils atomar vor, nicht molekular wie auf der Erde?
Wie rotiert eine Galaxie?
Welche Arten von Galaxien gibt es und wodurch werden sie unterschieden?
Mit Rotation haben Sie sich bestimmt schon oft beschäftigt, zumindest mit der eines starren Körpers. Diese war dadurch gekennzeichnet, dass jeder Massepunkt mit jedem anderen starr verbunden ist, sodass sich der starre Körper mit einer konstanten Winkelgeschwindigkeit 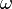 bewegt, für die Bahngeschwindigkeit
bewegt, für die Bahngeschwindigkeit 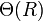 (Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie,
(Der Skalar R bezeichnet im Folgenden stets den Abstand eines Objektes, das sich in der Milchstraßenebene befindet, vom Zentrum der Galaxie, 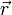 dagegen einen beliebigen Ortsvektor.) also gilt:
dagegen einen beliebigen Ortsvektor.) also gilt:
Etwas anders sieht das Verhalten von 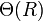 für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte
für astronomische Systeme wie die Milchstraße aus, die eben nicht starr verbunden sind und meist auch keine homogene Massendichte 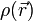 aufweisen. Für ein beliebiges
aufweisen. Für ein beliebiges 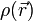 gilt in einem Gravitationspotential
gilt in einem Gravitationspotential 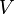 unter Ausnutzung des Virialsatzes (2T = V) die Beziehung:
unter Ausnutzung des Virialsatzes (2T = V) die Beziehung:
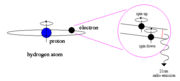
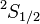 von F=1 nach F=0, der die Emission eines Photons mit der Frequenz
von F=1 nach F=0, der die Emission eines Photons mit der Frequenz 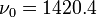 GHz zur Folge hat. Rechts: Das Termschema des Wasserstoffs mit den entsprechenden Hyperfeinstrukturniveaus.
GHz zur Folge hat. Rechts: Das Termschema des Wasserstoffs mit den entsprechenden Hyperfeinstrukturniveaus.