Hall-Effekt-Aufbau: Unterschied zwischen den Versionen
P Lab (Diskussion | Beiträge) K (→3. eventuelle Beleuchtung der Probe bei 4,2K / Illumination) |
P Lab (Diskussion | Beiträge) K |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:FKP_W_EdwinHall.jpg|miniatur|100px|Edwin Hall]] | [[Datei:FKP_W_EdwinHall.jpg|miniatur|100px|Edwin Hall]] | ||
1879 entdeckte Edwin Hall den nach ihm benannten Hall-Effekt. Dieser Effekt sieht wie folgt aus: | 1879 entdeckte Edwin Hall den nach ihm benannten Hall-Effekt. Dieser Effekt sieht wie folgt aus: | ||
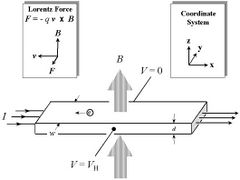
| − | Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so werden die in dem Leiter vorhandenen Ladungsträger durch die | + | Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so werden die in dem Leiter vorhandenen Ladungsträger durch die Lorentzkraft abgelenkt. Diese Ablenkung geschieht sowohl senkrecht zum Magnetfeld, als auch senkrecht zur Bewegungsrichtung der Ladungsträger. Durch abgelenkte Ladungsträger wird sich auf einer Seite des Leiters eine erhöhte Ladung aufbauen, so dass ein elektrisches Feld generiert wird, das der Lorentzkraft entgegenwirkt. Die mit dem elektrischen Feld einhergehende Spannung wird Hall-Spannung U<math>_\text{H}</math> genannt. |
== Was erhalte ich durch die Anwendung des Hall-Effekt-Aufbaus? == | == Was erhalte ich durch die Anwendung des Hall-Effekt-Aufbaus? == | ||
Verwendet man den Hall-Effekt-Aufbau so können aus Widerstands- und Spannungsmessungen folgende Halbleitermerkmale ermittelt werden: | Verwendet man den Hall-Effekt-Aufbau so können aus Widerstands- und Spannungsmessungen folgende Halbleitermerkmale ermittelt werden: | ||
| Zeile 43: | Zeile 43: | ||
# Speichern und eventuelles Drucken der Messergebnisse | # Speichern und eventuelles Drucken der Messergebnisse | ||
| − | Bevor die einzelnen Schritte im Detail beschrieben werden, können Sie im nachstehenden Bild die Hauptebene des | + | Bevor die einzelnen Schritte im Detail beschrieben werden, können Sie im nachstehenden Bild die Hauptebene des Programms ''Hall_Main_EXP2.vi'' sehen: |
{| | {| | ||
|[[Datei:FKP_W_HallA_Hauptbildschirm.png]] | |[[Datei:FKP_W_HallA_Hauptbildschirm.png]] | ||
| Zeile 57: | Zeile 57: | ||
Ferner kann man unter '''Temperature''' angeben bei welcher Probentemperatur die Messung durchgeführt wird (für gewöhnlich Raumtemperatur (RT) und in flüssigem Helium 4,2K (lHe)). | Ferner kann man unter '''Temperature''' angeben bei welcher Probentemperatur die Messung durchgeführt wird (für gewöhnlich Raumtemperatur (RT) und in flüssigem Helium 4,2K (lHe)). | ||
| − | Bei RT wird automatisch Magnetfeldquelle auf ''permanent'' geschaltet. Der Permanentmagnet hat eine Feldstärke von 123mT. Bei lHe wird die Magnetfeldquelle automatisch auf ''coil'' geschaltet. Da diese Messung innerhalb einer Heliumkanne durchgeführt wird und am Lehrstuhl für ''Angewandte Festkörperphysik'' zwei verschiedene gibt, muss man im erscheinenden Fenster zwischen normalleitender und | + | Bei RT wird automatisch Magnetfeldquelle auf ''permanent'' geschaltet. Der Permanentmagnet hat eine Feldstärke von 123mT. Bei lHe wird die Magnetfeldquelle automatisch auf ''coil'' geschaltet. Da diese Messung innerhalb einer Heliumkanne durchgeführt wird und am Lehrstuhl für ''Angewandte Festkörperphysik'' zwei verschiedene gibt, muss man im erscheinenden Fenster zwischen normalleitender und supraleitender Spule wählen. Man findet am Kannenhals die Art der sich in der Heliumkanne befindlichen Spule. |
Diese Angaben werden letztlich mit den Messergebnissen abgespeichert, um die Messergebnisse eindeutig zuordnen zu können. | Diese Angaben werden letztlich mit den Messergebnissen abgespeichert, um die Messergebnisse eindeutig zuordnen zu können. | ||
| Zeile 91: | Zeile 91: | ||
[[Datei:FKP_W_HallA_Schichtwiderstand.PNG|thumb|]] | [[Datei:FKP_W_HallA_Schichtwiderstand.PNG|thumb|]] | ||
Wie oben bereits erwähnt ist die Ermittlung des Schichtwiderstandes <math>\text{R}_\text{S}</math> Bestandteil der Van-der-Pauw-Technik. | Wie oben bereits erwähnt ist die Ermittlung des Schichtwiderstandes <math>\text{R}_\text{S}</math> Bestandteil der Van-der-Pauw-Technik. | ||
| − | Es wird der festgelegte Strom angezeigt, die Kontaktkonfiguration der Messung (S21M34 bedeutet z.B., dass durch die Kontakte 2-1 der Strom fließt ('''S'''ource) und zwischen den Kontakten 3-4 der Widerstand gemessen wird ('''M'''easure)), ferner wird der dazugehörige Spannungsabfall und als Resultat der Messung der | + | Es wird der festgelegte Strom angezeigt, die Kontaktkonfiguration der Messung (S21M34 bedeutet z.B., dass durch die Kontakte 2-1 der Strom fließt ('''S'''ource) und zwischen den Kontakten 3-4 der Widerstand gemessen wird ('''M'''easure)), ferner wird der dazugehörige Spannungsabfall und als Resultat der Messung der Schichtwiderstand angegeben. |
Man kann die Messung mittels '''Measure''' beliebig oft wiederholen und mittels '''OK''' verlassen. | Man kann die Messung mittels '''Measure''' beliebig oft wiederholen und mittels '''OK''' verlassen. | ||
Version vom 3. August 2009, 12:46 Uhr
1879 entdeckte Edwin Hall den nach ihm benannten Hall-Effekt. Dieser Effekt sieht wie folgt aus:
Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so werden die in dem Leiter vorhandenen Ladungsträger durch die Lorentzkraft abgelenkt. Diese Ablenkung geschieht sowohl senkrecht zum Magnetfeld, als auch senkrecht zur Bewegungsrichtung der Ladungsträger. Durch abgelenkte Ladungsträger wird sich auf einer Seite des Leiters eine erhöhte Ladung aufbauen, so dass ein elektrisches Feld generiert wird, das der Lorentzkraft entgegenwirkt. Die mit dem elektrischen Feld einhergehende Spannung wird Hall-Spannung U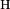 genannt.
genannt.
Inhaltsverzeichnis
- 1 Was erhalte ich durch die Anwendung des Hall-Effekt-Aufbaus?
- 2 Physikalischer Hintergrund
- 3 Softwareanwendung
- 3.1 1. Eingabe globaler Daten / Global settings
- 3.2 2. Wahl des elektrischen Stromes / Auto current
- 3.3 3. eventuelle Beleuchtung der Probe bei 4,2K / Illumination
- 3.4 4. Kontaktkontrolle / Check contacts
- 3.5 5. Bestimmung des Schichtwiderstandes / Resistivity
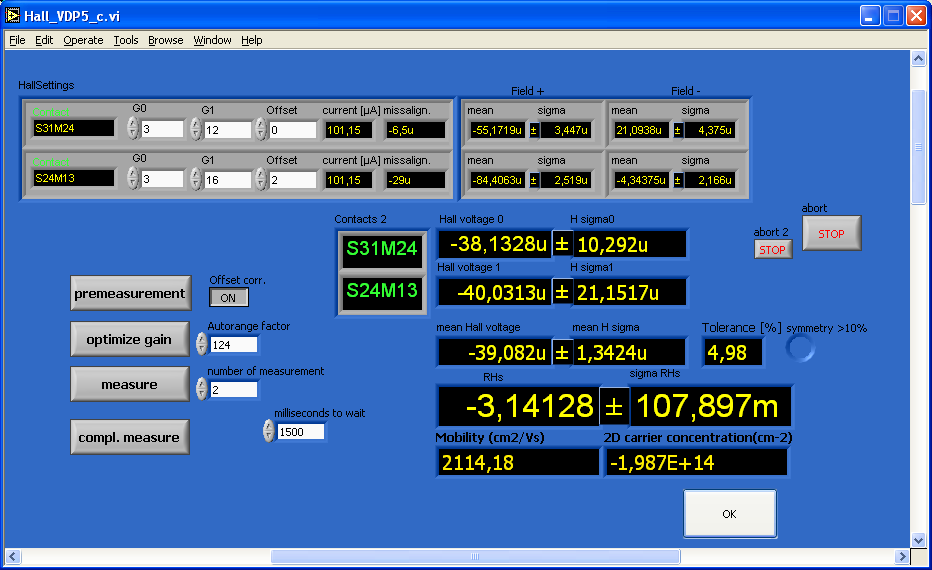
- 3.6 6. Messung der Hall-Spannung / Hall meas.
Was erhalte ich durch die Anwendung des Hall-Effekt-Aufbaus?
Verwendet man den Hall-Effekt-Aufbau so können aus Widerstands- und Spannungsmessungen folgende Halbleitermerkmale ermittelt werden:
- Flächenladungsträgerdichte n (
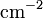 )
) - Mobilität µ (
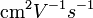 )
) - Schichtwiderstand R
 (
(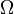 )
) - Hallspannung U
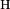 (V)
(V) - Mittlere freie Weglänge
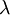 (µm)
(µm)
Die Messung kann bei Raumtemperatur (RT) und bei 4,2K (liquid Helium (lHe)) und jeweils im Dunkeln sowie unter Beleuchtung durchgeführt werden.
Physikalischer Hintergrund
Der Hall-Effekt kann, wie oben beschrieben, dazu ausgenutzt werden die Ladungsträgerdichte in Halbleitern zu bestimmen. Hierzu macht man folgende theoretische Überlegungen: Der Lorentzkraft wirkt ein elektrisches Feld entgegen, so dass bei Kompensation folgendes gilt:
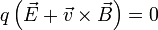
Mit der Wahl des Koordinatensystems, in dem sich die Elektronen in x-Richtung bewegen und das Magnetfeld in z-Richtung zeigt, ergibt sich 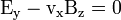 , was mit der Stromdichte
, was mit der Stromdichte 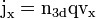 zu Folgendem führt:
zu Folgendem führt:
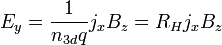
wobei 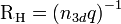 die Hall-Konstante ist. Mit
die Hall-Konstante ist. Mit 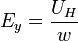 , wobei w die Breite der Schicht ist, und mit
, wobei w die Breite der Schicht ist, und mit 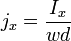 , wobei d die Dicke der Schicht ist, folgt die Hallspannung
, wobei d die Dicke der Schicht ist, folgt die Hallspannung 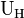 und eine Vorschrift für die Ladungsträgerdichte:
und eine Vorschrift für die Ladungsträgerdichte:
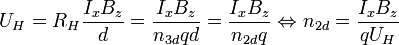
Um also die Flächenladungsträgerdichte zu ermitteln muss man die Hall-Spannung messen. Der Strom wird selbst bestimmt, das Magnetfeld ist bekannt und durch das Vorzeichen von 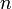 lässt sich feststellen, ob die Probe n- bzw. p-leitend ist (Vorzeichen von q).
lässt sich feststellen, ob die Probe n- bzw. p-leitend ist (Vorzeichen von q).
Ferner lässt sich über eine Hall-Messung ebenfalls die Beweglichkeit µ über den Schichtwiderstand 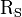 und Hall-Spannung bzw. Flächenladungsträgerdichte bestimmen. Der Zusammenhang sieht wie folgt aus:
und Hall-Spannung bzw. Flächenladungsträgerdichte bestimmen. Der Zusammenhang sieht wie folgt aus:
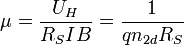
Die Messung des Schichtwiderstandes ist Bestandteil der Van-der-Pauw-Technik.
Softwareanwendung
Die Anwendung der Software gliedert sich in ca. sieben Schritte:
- Eingabe globaler Daten
- Wahl des elektrischen Stromes
- eventuelle Beleuchtung der Probe bei 4,2K
- Kontaktkontrolle
- Bestimmung des Schichtwiderstandes
- Messung der Hall-Spannung
- Speichern und eventuelles Drucken der Messergebnisse
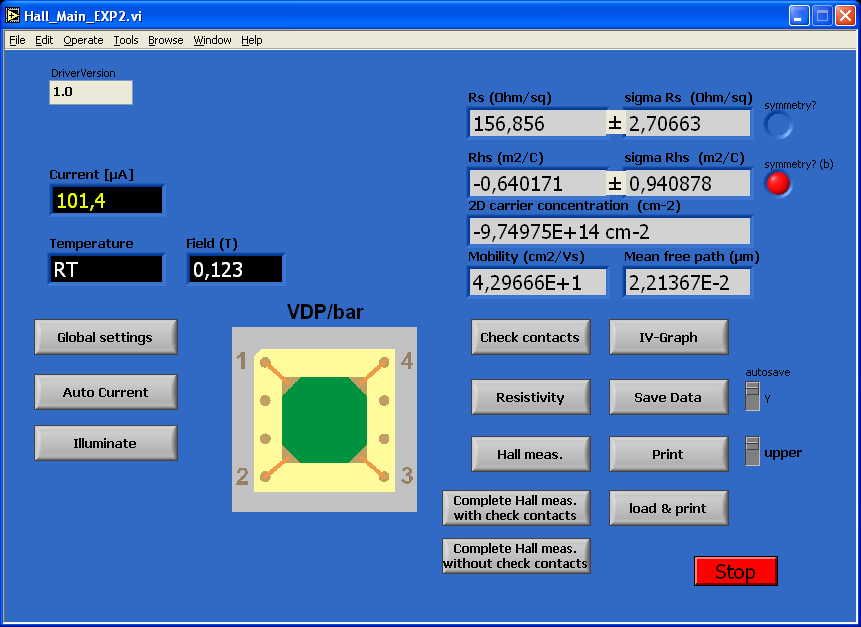
Bevor die einzelnen Schritte im Detail beschrieben werden, können Sie im nachstehenden Bild die Hauptebene des Programms Hall_Main_EXP2.vi sehen:
|
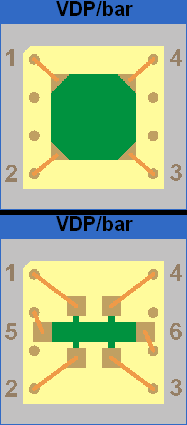
Von der Hauptebene des Programms kommt man zu den Voreinstellungen (Global settings, Auto Current, Illuminate), zu den Messvorgängen (Check contacts, Resistivity, Hall measurement, IV-Graph) und der Speicherung der Messergebnisse (Save Data, Print). Die einzige direkte Einstellmöglichkeit auf der Hauptebene ist die Festlegung der Probengeometrie: Hier kann man zwischen Van-der-Pauw- und Bar-Geometrie wählen, indem man auf das Bild unter VDP/bar klickt. Die Zahlen auf den Bildern spiegeln die Kontaktorientierung wider, die zum Anschluss der Kontakte an die Hardware wichtig ist.
1. Eingabe globaler Daten / Global settings
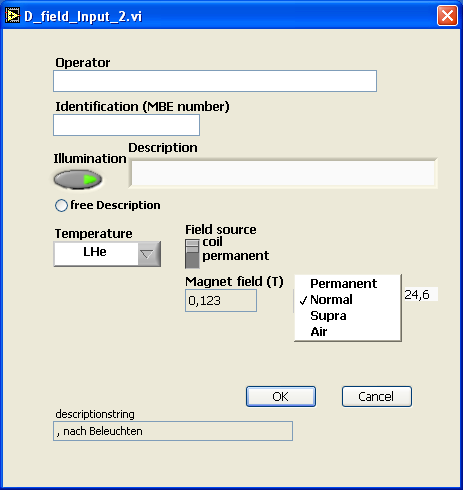
Die globalen Daten dienen dazu die Messergebnisse einer bestimmten Probe zuzuordnen und anzugeben unter welchen Bedingungen gemessen wurde. Im Feld Operator gibt man seinen Namen ein, in Identification (MBE number) gibt man die Probennummer ein, die jeder Halbleiterprobe vorab vergeben wird, in Description kann man eine nähere Beschreibung zur Messung angeben. Der Schalter Illumination gibt an, ob die Messung unter Beleuchtung (grün leuchtet auf) oder in Dunkelheit durchgeführt wird. Ferner kann man unter Temperature angeben bei welcher Probentemperatur die Messung durchgeführt wird (für gewöhnlich Raumtemperatur (RT) und in flüssigem Helium 4,2K (lHe)).
Bei RT wird automatisch Magnetfeldquelle auf permanent geschaltet. Der Permanentmagnet hat eine Feldstärke von 123mT. Bei lHe wird die Magnetfeldquelle automatisch auf coil geschaltet. Da diese Messung innerhalb einer Heliumkanne durchgeführt wird und am Lehrstuhl für Angewandte Festkörperphysik zwei verschiedene gibt, muss man im erscheinenden Fenster zwischen normalleitender und supraleitender Spule wählen. Man findet am Kannenhals die Art der sich in der Heliumkanne befindlichen Spule.
Diese Angaben werden letztlich mit den Messergebnissen abgespeichert, um die Messergebnisse eindeutig zuordnen zu können.
2. Wahl des elektrischen Stromes / Auto current
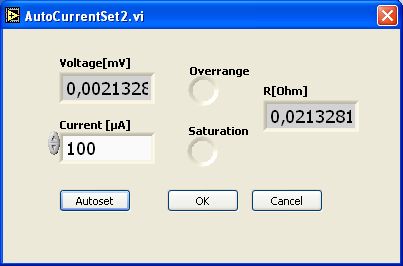
Für die Messung des Hall-Effektes kann in dieser Ebene der Strom festgelegt werden. Mit dem Button Autoset wird für die benutzte Halbleiterprobe der Strom gesetzt, bei dem 25mV an den Kontakten abfällt. Man kann allerdings den Strom in der Box Current [µA] selbst festlegen. Der Strom wird in µA angegeben und liegt für Standard-Hallproben bei 100µA. Mit OK bestätigt man die Festlegung des Stromes für die Messung/en.
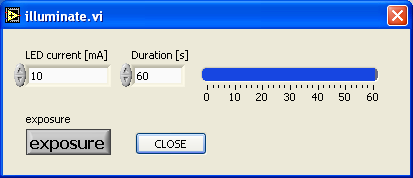
3. eventuelle Beleuchtung der Probe bei 4,2K / Illumination
In dieser Ebene kann man die Halbleiterprobe mit einer LED, die man in den Probenhalter installiert hat, beleuchten. Mit dieser Beleuchtung forciert man die Erhöhung der Ladungsträgerdichte durch Fundamentalabsorption. Der LED-Strom ist für gewöhnlich 10mA, die Dauer der Beleuchtung kann selbst eingestellt werden. Hat man den LED-Strom und die gewünschte Beleuchtungsdauer eingestellt, so kann man über exposure den Beleuchtungsvorgang starten.
Hinweis: Die Dauer der Beleuchtung wird allerdings nicht automatisch abgespeichert; es ist also ratsam die Dauer oder die Gesamtdauer der Beleuchtung in Global settings  Description einzugeben.
Description einzugeben.
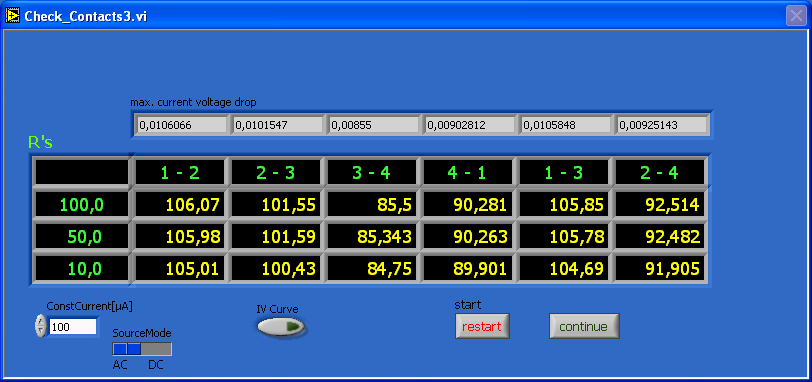
4. Kontaktkontrolle / Check contacts
Die auf der Probe aufgedampften Strukturen sind für gewöhnlich sehr klein und werden mittels eines dünnen (Durchmesser 30µm) Aluminium-Bond-Drahtes mit Pads eines Chipträgers / Chipcarriers verbunden. Ob die Strukturen auf der Probe mit den Pads des Chipcarriers gut verbunden sind und um festzustellen wie die Unterschiede in Hinblick des Widerstandes zwischen den Kontakten sind, kann in dieser Ebene festgestellt werden. Die grünen Zahlen auf der linken Seite (100, 50, 10) spiegeln den Messstrom wider (100%, 50%, 10% des festgelegten Stromes), die oberhalb der gelben Zahlen (1-2, 2-3, 3-4 usw.) geben an zwischen welchen beiden Kontakten der Widerstand gemessen wird (s. oben VDP/bar). Die Tabelle mit den gelben Zahlen sind dann folglich die gemessenen Widerstandswerte und geben auch Auskunft über die Symmetrie der Probe. Für den Fall, dass sich z.B. ein Bond-Draht (aufgrund der Abkühlung auf 4,2K und der einhergehenden Kontraktion des dünnen Bond-Drahtes) von der Probe oder dem Pad löst oder gar reißt, kann hier festgestellt werden, ob die weiteren Messungen noch Sinn machen.
5. Bestimmung des Schichtwiderstandes / Resistivity
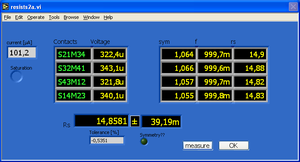
Wie oben bereits erwähnt ist die Ermittlung des Schichtwiderstandes 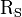 Bestandteil der Van-der-Pauw-Technik.
Es wird der festgelegte Strom angezeigt, die Kontaktkonfiguration der Messung (S21M34 bedeutet z.B., dass durch die Kontakte 2-1 der Strom fließt (Source) und zwischen den Kontakten 3-4 der Widerstand gemessen wird (Measure)), ferner wird der dazugehörige Spannungsabfall und als Resultat der Messung der Schichtwiderstand angegeben.
Man kann die Messung mittels Measure beliebig oft wiederholen und mittels OK verlassen.
Bestandteil der Van-der-Pauw-Technik.
Es wird der festgelegte Strom angezeigt, die Kontaktkonfiguration der Messung (S21M34 bedeutet z.B., dass durch die Kontakte 2-1 der Strom fließt (Source) und zwischen den Kontakten 3-4 der Widerstand gemessen wird (Measure)), ferner wird der dazugehörige Spannungsabfall und als Resultat der Messung der Schichtwiderstand angegeben.
Man kann die Messung mittels Measure beliebig oft wiederholen und mittels OK verlassen.