Hall-Effekt-Aufbau

Edwin Hall

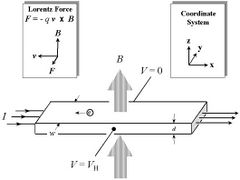
1879 entdeckte Edwin Hall den nach ihm benannten Hall-Effekt. Dieser Effekt sieht wie folgt aus: Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so werden die in dem Leiter vorhandenen Ladungsträger durch die Loretzkraft abgelenkt. Diese Ablenkung geschieht sowohl senkrecht zum Magnetfeld, als auch senkrecht zur Bewegungsrichtung der Ladungsträger. Durch abgelenkte Ladungsträger wird sich auf einer Seite des Leiters eine erhöhte Ladung aufbauen, so dass ein elektrisches Feld generiert wird, das der Lorentzkraft entgegenwirkt. Die mit dem elektrischen Feld einhergehende Spannung wird Hall-Spannung U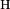$_\text{H}$ gennant.

Was erhalte ich durch die Anwendung des Hall-Effekt-Aufbaus?

Verwendet man den Hall-Effekt-Aufbau so können aus Widerstands- und Spannungsmessungen folgende Halbleitermerkmale ermittelt werden:

• Flächenladungsträgerdichte n ($\text{cm}^{-2}$ )
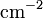• Mobilität µ ($\text{cm}^2\text{Vs}^{-1}$)
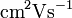• Schichtwiderstand R$_\text{S}$ ($\Omega$)
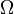• Hallspannung U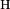$_\text{H}$ (V)
• Mittlere freie Weglänge 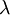$\lambda$ (µm}

Die Messung kann bei Raumtemperatur (RT) und bei 4,2K (liquid Helium (lHe)) und jeweils im Dunkeln sowie unter Beleuchtung durchgeführt werden.

Physikalischer Hintergrund

Hall-Effekt

Der Hall-Effekt kann, wie oben beschrieben, dazu ausgenutzt werden die Ladungsträgerdichte in Halbleitern zu bestimmen. Hierzu macht man folgende theoretische Überlegungen: Der Lorentzkraft wirkt ein elektrisches Feld entgegen, so dass bei Kompensation folgendes gilt:

$q\left(\vec E + \vec v \times \vec B\right) = 0$

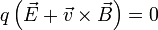
Mit der Wahl des Koordinatensystems, in dem sich die Elektronen in x-Richtung bewegen und das Magnetfeld in z-Richtung zeigt, ergibt sich 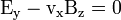$\text{E}_\text{y}-\text{v}_\text{x}\text{B}_\text{z} = 0$, was mit der Stromdichte 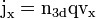$\text{j}_\text{x} = \text{n}_{\text{3d}}\text{q} \text{v}_\text{x}$ zu Folgendem führt:

$E_y = \frac{1}{n_{3d}q}j_xB_z = R_Hj_xB_z$

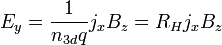
wobei 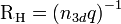$\text{R}_\text{H} = \left(n_{3d} q\right)^{-1}$ die Hall-Konstante ist. Mit 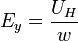$E_y=\frac{U_H}{w}$, wobei w die Breite der Schicht ist, und mit 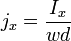$j_x = \frac{I_x}{wd}$, wobei d die Dicke der Schicht ist, folgt die Hallspannung 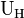$\text{U}_\text{H}$ und eine Vorschrift für die Ladungsträgerdichte:

$U_H = R_H\frac{I_xB_z}{d} = \frac{I_xB_z}{n_{3d}qd}=\frac{I_xB_z}{n_{2d}q}\Leftrightarrow n_{2d}=\frac{I_xB_z}{qU_H}$

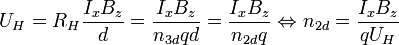
Um also die Flächenladungsträgerdichte zu ermitteln muss man die Hall-Spannung messen. Der Strom wird selbst bestimmt, das Magnetfeld ist bekannt und durch das Vorzeichen von 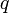$q$ lässt sich feststellen, ob die Probe n- bzw. p-leitend ist.

Ferner lässt sich über eine Hall-Messung ebenfalls die Beweglichkeit µ über den Schichtwiderstand 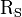$\text{R}_\text{S}$ und Hall-Spannung bzw. Flächenladungsträgerdichte bestimmen. Der Zusammenhang sieht wie folgt aus:

$\mu = \frac{U_H}{R_SIB} = \frac{1}{qn_{2d}R_S}$

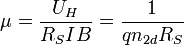
Die Messung des Schichtwiderstandes ist Bestandteil der Van-der-Pauw-Technik.